Among the thousands of volumes held and once held, by the Bendectine monastery at Melk, is a bound assortment of manuscripts that dates from the Renaissance. Once Codex Melk 794, this volume is now Codex Yale 24 and belongs to Yale University. The change of ownership was precipitated by monasteries being caught between diminishing financial returns on the land they owned and rising costs. Between the two world wars, numerous monasteries in Europe were forced to sell precious manuscripts from their libraries to dealers who then sold them on to libraries and museums in the United States. Thus in 1937, Codex Melk 794 left the shelf on which it had stood since the Baroque rebuilding of the monastery and was sold to a dealer who sold it on to the neurosurgeon and book-collector, Harvey Cushing. That same year, Cushing bequeathed the newly acquired codex to Yale University along with the rest of his not unsubstantial collection. Becoming Codex Yale 24, the volume is a part of the Harvey Cushing/John Hay Whitney Medical Library and may be seen online at: https://findit.library.yale.edu.

The works of the codex are mostly concerned with astronomy, the calendar and on how to make and use instruments such as the quadrant and the astrolabe. Of the thirty-two works, two are by Johannes of Gmunden (1380/1384-1442), eight are by Georg Aunpekh, generally known as Georg von Peuerbach (1423-1461) and two are by Johannes Müller of Königsberg, known as Regiomontanus (1436-1476). This trio of hugely important astronomers form the core of what is known as the First Viennese School of Astronomers and Mathematicians and during the Renaissance, the monastery at Melk had contacts both with this school and with the University of Vienna. Towards the end of the collection there is a text by the theologian, philosopher and mathematician, Nicholas of Cues, who, otherwise known as Cusanus (1401-1464), was a cardinal and the Bishop of Brixen. For a partial, hand-written index see pages i and ii: https://findit.library.yale.edu. The most striking image of the codex is a summary of Peuerbach’s classification of the nine different types of comet.

In what follows, with reference to Codex Yale 24, the world of Renaissance astronomy and instrument-making is introduced. To this effect, the practical knowledge necessary for the construction of instruments such as the quadrant and astrolabe is given – along with the reasoning that results in this knowledge being applicable to the situations concerned. In both cases, it is found that when it comes to the discerning of time, non-Euclidean geometry is involved so that both instruments look forward and back; back at an old way of thinking about and dealing with time and forward as they anticipate a whole new way of thinking about geometry and thus also of time. In the case of the old quadrant, the underlying construction even provides one of the methods by which non-Euclidean geometry is investigated. Doubts about whether, in the account of geometry given by Euclid, something had not been left out, were first voiced during the 1450’ies and are related to the doubts on Euclidean geometry that are tacitly raised by both the quadrant and the astrolabe. Thus in what follows, Parts I and II show and describe how, using nothing but a ruler and compass, an elevation and a plan of the Celestiel Sphere may be drawn up and how from them, the old and new quadrants and an astrolabe may be constructed. Thereafter, the key figures of the First Viennese School of Astronomers and Mathematicians are introduced along with some of the quadrants, astrolabes and other instruments that they made (Parts III, VIII, IX and X). In Part VIII the relation between the geometries of the astrolabe and quadrant and non-Euclidean geometry is explored. In Parts IV-VII the basic theology mathematical aspects of „The Controversy of the Doctrine of Ignorance“ are introduced. This includes the endeavours of one of the most prominent participants of the controversy at squaring the circle along with the replies of the First Viennese School of Astronomers and Mathematicians. Part IX tells the story of the School’s connection to Melk and the historic observation made there in 1457. Part X introduces an exiled Greek cardinal and his connections to the School. Moving on from this, Part XI raises the possibility of there being a connection between the School and Piero della Francesca, who also used mathematics as a way of approaching God and had his own way of squaring the circle. As the name says, the Laboratorium geometricum mellicensis is a laboratory where within a historical context, geometrical and mathematical questions are asked and research is conducted. Despite the historical context research is conducted with an eye to our own situation and the answers arrived are seen as being relevant to us today. In areas where detail is lacking, this either because the object or topic under discussion is a matter of on-going investigation or because the paper covering the insights has not yet been published.

As nothing comes from nothing (for as Julie Andrews sings in The Sound of Music, „nothing ever could“) this article is dedicated to the memory Peter I. Drinkwater of Shipton-on-Stour, who instructed the present author in the geometry of the astrolabe and who is the author of a number of booklets on sundial construction.

He is also the author of a booklet that is concerned with the sundials of Nikolaus Kratzer, who after spending time at the Austrian Charterhouse of Mauerbach, went to England where he became dialist to Henry VIII. In the famous portrait by Holbein entitled, The Ambassadors, astronomical instruments made by Kratzer are depicted and in his booklet, Drinkwater subjects them to detailed scrutiny.

Thus like the present author, Peter Drinkwater shows that there is sometimes more going on in a Renaissance painting than art historians care to admit.

I. TWO KINDS OF ANALEMMA, THE ORGANUM PTOLEMEI AND THE OLD QUADRANT

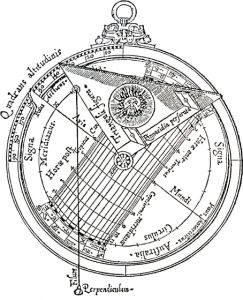
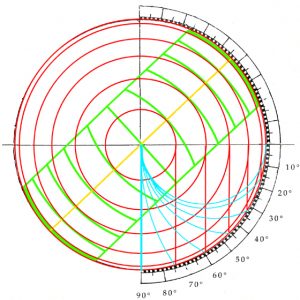
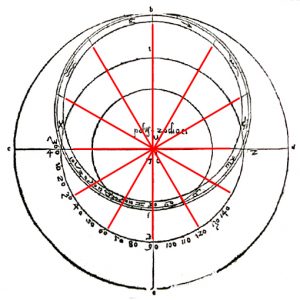
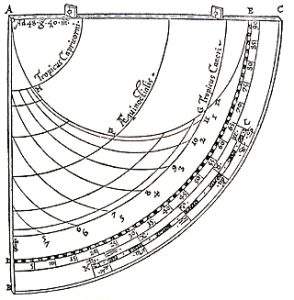
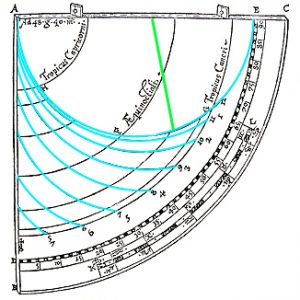
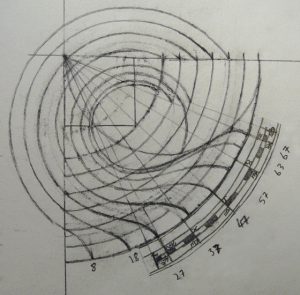
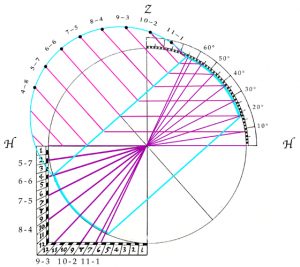
Formed from a quarter of a circle, in its simplist form a quadrant enables the angular height of the sun in the sky to be measured and converted into the time of day. In Codex Yale 24 there is one treatise on the quadrant that begins on page 202, https://findit.library.yale.edu and two tracts on what is known as an organum Ptolemei which is the construction that lies behind the quadrant. These begin on pages 267 https://findit.library.yale.edu and 446  https://findit.library.yale.edu, with the second having a diagram on the page 447. Yet behind the organum Ptolemei there is the analemma or „Master Diagram“ of instrument-making. This is an elevation of a geocentic model of the world in which the Ecliptic is shown as a slanting mid-section of a circle. On the diagram below, where „Z“ stands for „zenith“ and indicates the point in the sky directly above an observer, „H“ indicates the horizon with the grey area being the surface of the Earth below which the sun sets during the hours of night. As the sun rises from below the horizon on the left, it ascends up towards the right to obtain a maximum height at midday before then following exactly the same path back down towards a nadir that represents midnight. The outer limits of the Ecliptic, which contains these paths of rising and setting  is shown in turquoise, with the red and blue lines at the top and bottom indicating the paths followed by the sun on the days of the summer solstice (red) and the winter solstice (blue). The yellow lines in between show the paths followed on the days when the sun enters a new sign of the Zodiac.

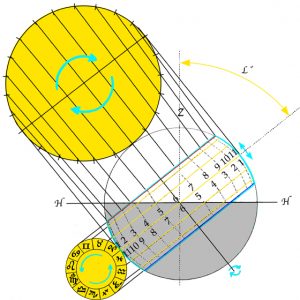
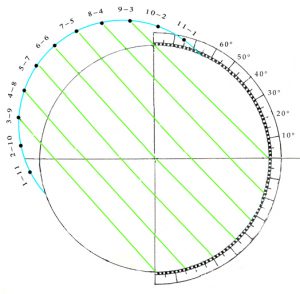
On the diagram, the largest circle of movement is that indicated by the central yellow line that shows the path of the sun on the day of the equinoxes. This is also the diameter of the enclosing circle and the diameter of the hidden circles that dictate the way that the hour lines are curved, as at the same time of day, at different times of the year, the sun is to be seen at different heights in the sky. If the two circles of motion shown in yellow are halved and the hours and signs of the Zodiac are both doubled-up and shown in pairs, then the diagram can be compacted to form an analemma from which all else follows. On a side elevation of the celestiel sphere, the organum Ptolomei is the band of the ecliptic that contains the sun’s motion. As the projection is effectively one made from infinity, the distorting effects of perspective are negated and the projection can be used as the basis for a number of instruments. The construction is made by carrying the hours lines  down and using the points where they cross the lines of the diagonally slantling eliptic, to define arcs (shown in green) that represent the position throughout the year of the sun at the time of day concerned.

Where the great circle that links midday and midnight coincides with the circle that bounds the whole, as one works inwards from 1-11 towards 5-7, the ellipses become ever more pointed, until at six o’clock the elevation shows them as a single straight line. Working inwards, it can also be seen that the arcs of the circles formed by joining the two points together increasingly fail to coincide with the ellipses (shown in red) of the great circles that they are supposed to reproduce. Nevertheless, as ellipses are difficult for instrument-makers to draw, despite the inaccuracies incurred, the arcs of circles are used.

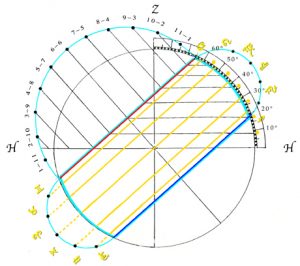
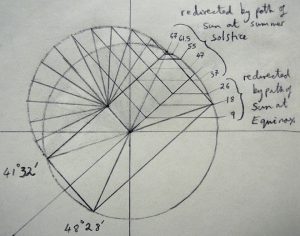
To set an analemma for the Latitude, L, of the observer, the axis of the Ecliptic is tilted by 90° minus L. This means that at the Equator, as 90° – 0° = 90°, the Ecliptic stands at right-angles to the observer’s horizon so that day and night are always of equal length and with there are no seasons. With increasing Latitude, the Ecliptic is progressively pushed down until at the North Pole (90°), it is parallel with the plane of the observer’s horizon and the summer sun provides light 24 hours a day, while in the winter, it is invisible for months on end.

In between these extremes, the observer’s latitude, read from the zenith downwards, indicates the path of the sun at the time of the equinoxes. This is when the sun’s path passes through the centre point of the main circle. From this point the extent of the Ecliptic is established by counting out 23.5° in both directions. In his Almgest, the Ecliptic was defined by Ptolemy as being 23° 51′ 20“ in extent. This was arrived at by measuring the height of the sun at noon on the day of the equinoxes and then subtracting this from its height at noon on the day of the summer solstice. Today the inclination of the Ecliptic is seen as varying between 22.1° and 24.5° as the tilt of the Earth’s axis follows a 41.000 year cycle. The value used by Regiomontanus was 23.5° which is close to the current value of 23° 26′ and a varying number of seconds. The proximity of 23.5° to 24° and the even closer proximity of the value arrived at by Ptolemy, puts into context the value inherent in the rule of thumb method of constructing an analemma given by Vitruvius, in his Ten Books of  Architecture. Here the instruction is to divide a the circle of the Celestiel Sphere into fifteen and to use one part (=24°) as the inclination of the Ecliptic. As Vitruvius‘ work was a much read book during the Renaissance, for many, the inclination of the Ecliptic was either seen as being 24° or as a divinely orchestrated approximation to 24° with the significance of this being discussed below in the Part IX.

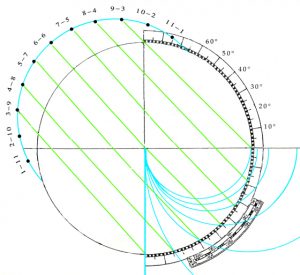
If along the red line of the sun’s journey on the day of the summer solstice, the parallel lines drawn through the points that mark the hours are turned and diverted so as to run parallel to the observer’s horizon, then the height of the sun at the corresponding hour of the day can be read off on the scale at the points indicated on the diagram below by the yellow dots. Equally the same can be done for the winter solstice and the days when the sun enters a new sign of the Zodiac.

Conversely, from the height of the sun, using an organum Ptolemei the time of day may be ascertained. This is shown in a book on dial-making written by Orance Finé (1494-1555) who made sun-dials and other instruments for Francis I of France. Like a quadrant, this adapted version of the organum Ptolemei is fitted with sighting-vanes and is given in his Second Book of Solar Horology with reproductions of the illustrations and a commentary being published in the early 1990’ies by Peter I. Drinkwater, it being from this work that the drawings of quadrants and practical commentaries are taken whilst the theoretical foundations and their ramifications are deductions by Alexander Curtis. Following Ernst Zinner, the organum Ptolemei was adapted for use as a sundial not by Finé but either by Peuerbach or Regiomontanus, with the latter in any case engraving one on the reverse side of an astrolabe that he made for Cardinal Bessarion in 1462.

To use the adapted version of the organum Ptolemei, the pointer on the rotating inner plate on which the organun Ptolemei is engraved, is set to the observer’s Latitude. The triangular sighting vane is then aligned with the sun so that a golden glow of light shines through the outer sight to illuminate its counterpart on the inside. The day of the year in the calendar is then converted into the position of the sun in degrees on the Zodiac. From this the solar declination, which is the height of the sun above the Celestriel Equator on the day concerned, can be read off and it is from this point, that the closest hour-line or pair of hour-lines are followed up towards the string of the pendulum, with the point where their interpolation meets the string being the time of day.

The organum Ptolemei is particularly suited for use on the reverse side of an astrolabe, where the projection on the obverse side requires a whole circle, so that if no other features are required on the reverse side, the organum Ptolemei can be shown in its entirity without having to be compressed or reduced in any way. On a quadrant however this is not possible and the organum Ptolemei must be shrunk into the space of a quarter circle. This is achieved by extending the parallel lines that mark the hours, down into the lower right-hand quarter so that they divide the quarter circle into six, 15° intervals. These are then doubled-up so that the quarter circle encompasses the twelve hours of daylight.

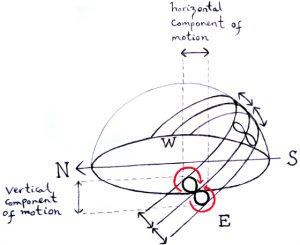
On a quadrant, the sighting vanes are mounted on the upper edge of the lower quarter circle, whilst from the right-angle which is the centre of the containing circle, a pendulum hangs down with a marker. To use the instrument, the sighting vanes are aligned with the sun so that as the pendulum hangs down, the marker indicates the hour of day via the hour-lines. The problem is that due to the tilt of the Eliptic and the varying rate at which the sun appears to move through the sky, the hour-lines carried down do not take account of seasonal variations which cause the position of the sun at any given hour of the day to move from day to day as the seasons progress. This is due to the fact that as, with the approach of summer, the sun climbs higher in the sky and becomes visible for longer, so its position at a certain time of day shifts northwards, whilst following the summer solstice, its position then begins to shift back towards the South. The exception is twelve o’clock when the sun, although its height in the sky varies, is always due South of an observer. Except at twelve o’clock, when the sun is always due South of an observer, associated with this North-South motion there is an East-West component. These factors combine so that as the hours of the day approach twelve o’clock, the amount of East-West variation decreases whilst after midday it increases again to re-attain a maximum at six o’clock.

The straight lines of the hour-lines carried down must therefore be made into curves which, starting from the right-angle on the quadrant meet the outer scale at the points marked off every 15° with the curves approximately replicating the position of the at a given hour of day. Apart from at 12 o’clock, if plotted every day at the same time of day, the path of the sun in the sky will be found, over the course of a year, to describe an asymmetrical figure of eight. The asymmetrical nature of the figure reflects the fact that not only is the axis of the Earth as it rotates about itself tilted by the 23.5°, resulting in the tilt of the Ecliptic but also the fact that in orbiting around the sun, the Earth does not describe a circle but rather follows the path of an ellipse which has the sun at one of its two centres. This results in the sun appearing to move faster through the sky in autumn, winter and spring than it does in summer. Thus instead of crossing back on itself at the time of the equinoxes, the path of the sun meets itself at a point equivalent to late spring and late summer.

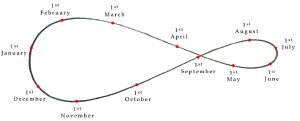
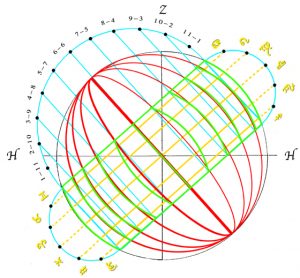
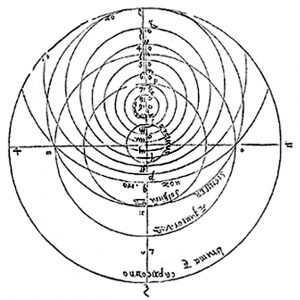
These paths in the sky are the second meaning of the word „analemma“ and are also traced out on the surface of any dial that over the course of a year maps out the sun’s daily motion in the sky. The dialist’s problem is therefore of devising hour-lines that as closely as possible replicate this motion. On the Celestiel Sphere, if the vertical components of motion are ignored, the variations in the position of the sun at each hour of the day from a mean position can be seen as following the segments, shown below in yellow, of a series of circles, shown in orange, that are wrapped at different heights around the celestial sphere and which run parallel to the observer’s horizon.

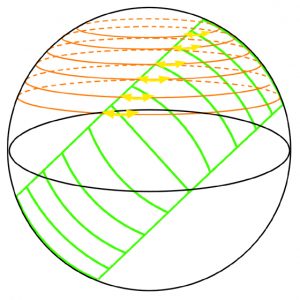
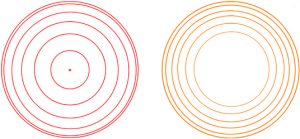
On the organum Ptolemei, as they have not been defined, nothing is known about these mean circles. Nevertheless their presence is testified to, when circles are drawn from the centre of the organum Ptolemei so as to pass through the points representing the sun at the different hours of the day at the time of the spring and autumn equinoxes. This results in the six concentric circles shown below in red and the operation can be seen as the result of a transformation that maps the hidden orange circles onto the red circles with it being in this way that the orange circles are indirectly testified to.

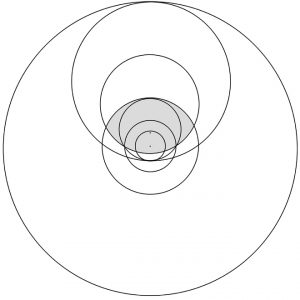
Following the transformation, the hidden orange circle of seasonal variation for 12 o’clock becomes the outer circle of the group of circles shown in red, while the other circles are progressively shrunk in a non-linear fashion that results in the 6 o’clock circle becoming an extensionless, infinitely compacted point.

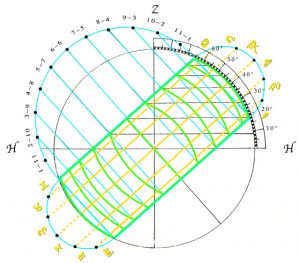
If this operation, which from the hidden circles makes the equinoxal hour circles, is inverted with the 6 o’clock circle, which is largest hidden circle becoming a circle with a diameter half that of the enclosing circle of the organum Ptolemei, then the other circles will be progressively enlarged out from this circle, until the 12 o’clock circle becomes a circle of infinite radius with a circumference that is a straight line, as shown below in turquoise.

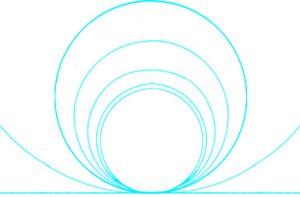
This progression takes place exponentially with the lack of curvature at 12 o’clock again reflecting the fact that at 12 o’clock, the sun is always due South of an observer so that there is no variation in where the 12 o’clock hour-line lies. The other arcs, increasing in curvature as they approach the six o’clock semi-circle, reflect the gradually increasing variation that the hour-lines are subject to, with the maximum being at 6 o’clock. On the quadrant to be, it is this second mapping that is used as the means by which the hour-lines are arrived at. Although the vertical component of motion associated with the sun’s changing position at any given hour of day, from day to day is ignored by both the orange and the turquoise circles, on a quadrant it is re-introduced by rotating the turquoise circles through 90° away from the horizontal plane onto the vertical plane, with the arcs of the circles giving an approximation to variations in height that the back and forth movement of the sun at any particular hour of day over the course of the year incurs. The rotation thus makes the 12 o’clock line the straight line of the circumferance of an infinite circle whilst the 6 o’clock line is a semi-circle that reflects a maximum of variation in position with respect to time.

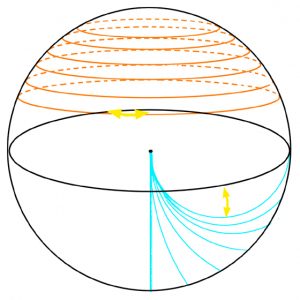
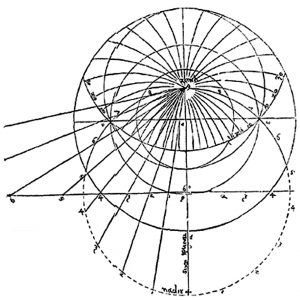
With the turquoise circles shown above halved, the point at which they converge is placed at the centre of the construction so that the points where the arcs of the circles meet the scale of the quadrant, do so at the points already indicated every 15° by the diagonally extended hour-lines. This results in the centres of the circles being spread out along the top edge of the quadrant and its continued extension away from the right-angle. Meanwhile, if from the series of red concentric circles considered above, lines are dropped down from where the circles cross the horizon, it will be found that they meet up with the 15° divisions already marked off.

Through the trick of rotating through 90°, the turquoise arcs take into account the vertical motion associated with the sun’s varying position over the year at any given hour of the day. Nevertheless, for this to work the sun’s position on the circle of the Zodiac must be introduced. This is done with reference to the observer’s Latitude and the position of the sun in the Zodiac. To this effect, the scale of the Zodiac on the organum Ptolemei is rotated in the vertical plane through 90° and adjusted so that it forms the arc of a circle that has a radius slightly larger than that of the scale of degrees. Mounted so that it is moveable, the mid-point of the scale is then aligned with the point on the degree scale that corresponds to 90° minus the Latitude of the observer.

This is the Co-Latitude and is the mean height of the sun at midday or in other words, the height of the sun at Equinox. The plumb-line is then pulled tight over the point on the Zodiac scale appropriate to the day in question (which is also the declination of the sun on that day) and a moveable bead is set at the point where the plumb-line crosses the semi-circle that marks the sixth hour. The altitude of the sun is then measured, with the position of the moveable bead on the plumb-line indicating local time as told in what horologists call „unequal hours“.

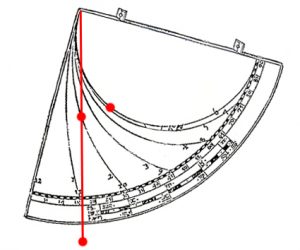
This means that with the passing of the winter solstice, the measured hours of the day, being unequal, get longer and longer, whilst following the summer solstice, they get progressively shorter. This results in extreme differences when the length of an hour in summer is compared with that of an hour in winter with the inverse applying to the hours of night. Equally in summer the hours of day are long whereas those of night are short with again, the inverse applying in winter. Already know as the „old“ quadrant in the Middle Ages, this form of quadrant is most accurate when the sun’s path in the sky is a semi-circle and this is also the time of year when the difference between the length of the hours of day and night are at their least divergent. At high Latitudes, away from the Equinoxes, a tolerable amount of inaccuracy is incurred. The old quadrant is universal and so, simply by adjusting the Zodiac scale to the Latitude of where one is, can be used any anywhere. For this reason, despite its for the modern mind, ungainly system of unequal hours, the old quadrant remained in use up until the fourteenth and fifteen centuries.

II. THE NEW QUADRANT AND THE PLANISPHERIC ASTROLABE

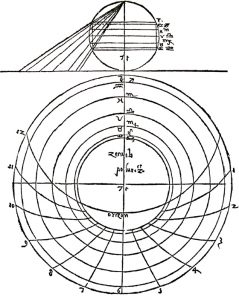
The so-called  „new quadrant“ was developed in Spain by Profatius during the thirteenth century and although the hour-lines of the new quadrant resemble those of the old quadrant, their means of derivation is completely different and is based on a system of projection known as stereographic projection. This means that the new quadrant is a derivative not of the analemma and organum Ptolemei but rather of the astrolabe. Where the analemma and organum Ptolemei are elevations of the Celestriel Sphere, a stereographic projection is a distended, non-linear plan and is the system of projection used on an astrolabe.

One of two astrolabes owned by the monastery at Melk (not on display)

In a stereographic system of projection lines are projected from a point on the globe conceived of as a sphere are followed through the sphere to a plane on the other side that is parallel with the sphere’s equator. On historical astrolabes this is the South Pole and the projection shows the North Pole as a point at the centre of the projection followed by the circles of the Tropic of Cancer, the Equator and the Tropic of Capricorn.

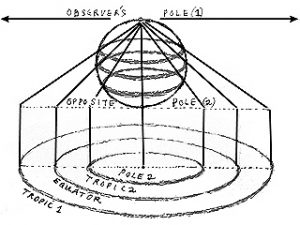
The South Pole meanwhile is flung out in all directions to infinity. While the great circles of Longitude become straight lines that extend out from the North Pole in all directions, the circles of Latitude that on the globe lie in-between the North and South Poles become circles, separated by ever increasing distances as the projection proceeds outwards. This first projection is an objective, global projection which is then juxtaposed and combined with a second system of projection that reflects the observer’s position on Earth. This second projection results in one line of longitude becoming a straight line whilst the rest become the segments of circles with large radii. The observer’s equivalent to lines of Latitude are called „lines of altitude“ by astronomers and „almucators“ by dialists and in the projection, although they are progressively enlarged, always remain circles, a significant number of which are shown in their entirety. Despite the linear distortions of distance that occur as one moves out away from the centre of the projection, angles and circles remain undistorted and it is this that enables the instrument to be used as a computing device that calculates angles and the differences between angles. In Codex Yale 24, information on how to construct an astrolabe is given by Christian de Prachatitz’s on pages 371-392 (https://findit.library.yale.edu), with the construction of circles of latitude and altitude being given on page 379: https://findit.library.yale.edu.

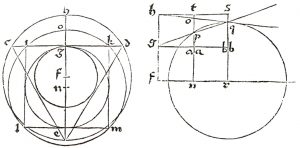
In Prachatitz’s text, following Medieval practice, the construction is conducted vertically, yet as the Patriarch of Aquileia, Danielle Barbaro, realised, this obscures an understanding of what is going on and so, in his masterfully instructive and wonderfully comprehensive work, The Practice of Perspective, the construction is presented horizontally.

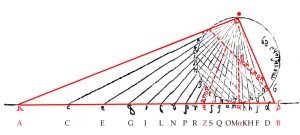
Diagram from Danielle Barbaro’s La pratica della perspettiva of 1569, page 171. Within triangle •,A,B, the three dotted lines show the observer’s horizon (labelled as „Eorizon“), the vertical axis, marked „α“ and the line that culminates in the observer’s zenith which is marked „z“ and is labelled „Zenith“

In Barbaro’s diagram the globe is shown with the circles of altitude, a, b, c, et cetera, for an observer at a position 22° North of the Equator. These are then projected onto a line that includes the base of the triangle the •,A,B and result in points A, B, C, et cetera. As can be seen, •,A,B is a right-angled triangle, with angle •,A,B being 22° and angle •,B,A being 68°. The inclination of the 90° angle at • is thus that which indicates how the 180° of altitude are to be distributed. For a position 0° North of the Equator the right-angled triangle is symmetrical and is tilted neither one way nor the other. This means that the triangle •,A,B spans is divided in half by the line marked „α“, that on the diagram lies between points M and K. Considering this shows how the so-called „tangent scale“ is integral to the projection. On the tangent scale, the 180° that lie between any two diametrically opposed points on the observer’s horizon embraces are condensed into 90°. To construct the almucators, the distance between A and B is divided in two and the point arrived at is used as the centre of a circle whose circumference passes through A and B. This circle defines the observer’s horizon. Smaller almucators are arrived at by successively adding the desired number of degrees to 22 on South side and subtracting from 22 on the North side. As before, the distance between pairs then gives the diameters of the ever decreasing almucators. Thus A is paired with B, C with D, E with F et cetera with J being missed out so that the pairing ends with R and S, between which there is Z. This latter is the observer’s zenith and is the point that lies directly above an observer and is found by subtracting the observer’s latitude from 90°. In this way, the Arctic Circle, the Tropic of Cancer, the Equator and the Tropic of Capricorn along with the observer’s horizon and almucators can be constructed.

From Danielle Barbaro’s La pratica della perspettiva of 1569, p. 172

In his Planispherium, Ptolemy recommends terminating a stereographic projection at the outermost point of what he calls the „largest invisible circle“. On a projection made from the South Pole this is the Antartic Circle. Yet Ptolemy’s recommendation is for the largest invisible circle to serve as a form of second horizon that indicates a boundary beyond which there are celestriel entities that regardless of the time of year, the observer will never be able to see, as for the Latitude where the observer is, they are blocked out by the curvature of the Earth.

Despite a compelling conceptual logic, prior to the charting of the stars of the Southern Hemisphere, the notion of terminating an astrolabe at the fatherest point of the largest invisible circle resulted in a lot of empty space. As this was impractical, all known astrolabes terminate the projection at the Tropic of Capricorn. An exception here is the organum described by Synesius of Cyrene. This was a device that used two steregraphic projections so as to convert the Celestriel co-ordinates advocated by Ptolemy into the degrees of altitude and ascention of an observer. On a reconstruction by Alexander Curtis it can be seen how the useful part of the plate shrinks in relation to the rest and how the then known constellations of the Southern Hemisphere become progressively distorted as one moves away from the centre, with Canis, for example, resembling a kangeroo.

On an astrolabe, the observer’s equivalent of lines of Longitude are called by dialists „gores of azimuth“ and are what astronomers call, „lines of ascension“. On the diagram below, the gores of azimuth are shown for an observer 22° North of the Equator. For Prachatitz’s version of the same on page 382 see: https://findit.library.yale.edu.

From Danielle Barbaro’s La pratica della perspettiva of 1569, p. 174

The gores of azimuth are arrived at by finding the centre of the arc that links the points where the Equator crosses the observer’s horizon. These points represent East (left) and West (right) and through them a circle is drawn. This is then divided into eighteen equal segments and a line is drawn from the centre that is parallel to the East-West axis. Using one half of the circle, lines are drawn that connect the zenith with the nine divisions of the circle. The points where these lines cross the line that runs through the circle’s centre are marked off and are then used as the centres of circles that pass through the zenith.

The often intricate and moveable rete shows the positions of the sun and stars as seen from the one of the poles. As the sun appears to have an additional form of motion to that which causes the movement of the stars, its changing position over the year is given by an eccentrically placed inner circle on the rete. This represents the Ecliptic which lies with one point on the Tropic of Cancer, whilst diametrically opposite, another point grazes the Tropic of Capricorn. Although each sign of the Zodiac is allocated 30°, the calibration is constructed and read off from the centre, with the eccentric positioning of the Elliptic resulting in an uneven scale. This reflects the fact that at different times in the year, the sun appears to move faster than at other times.

From Danielle Barbaro’s La pratica della perspettiva of 1569, p. 170

As the sun and stars rotate, the rete can be moved to replicate their changing positions relative to the observer’s zenith and horizon. In this way, the positions of stars at night can be ascertained along with the rising and setting times of the sun and stars for any day of the year.

To enable astrolabes to be used in different places, exchangeable plates were made for different Latitudes. An astrolabe therefore usually features a backing plate or mater, which has a frame or limb that encloses the exchangeable plates. The outer edge of the limb is calibrated in degrees and equal hours so that with a rule alignments may be set up and the desired calculations performed by the geometry of the instrument. On the reverse side, the mater is again calibrated with a scale of degrees so that by means of an alidade mounted in the middle, the heights of heavenly bodies in the sky can be measured. This is shown by Prachatitz at the beginning of his treatise on page 273:  https://findit.library.yale.edu. For Prachatitz’s diagram of the rete and limb on page 284, see: https://findit.library.yale.edu. The alidade also functions as a rule that on the inner scales, calendar dates can be  converted into positions on the Zodiac. In this way, the planispheric astrolabe combines objective and subjective points of view, so that the positions of stars and the sun at any given time can be ascertained or, from the height of a given body, the time may be read off. Among the pages of Codex Yale 24, there are is a second, unillustrated treatise by Prachatitz on the construction of the astrolabe (pages 275-281) which is followed by a treatise on the use of the instrument (pages 281-310). See: https://findit.library.yale.edu.

An astrolabe made by Alexander Curtis

To measure the height of the sun and set the astrolabe accordingly, the instrument is allowed to hang freely with the plate aligned in the direction of the sun. On the reverse side of the instrument, where the alidade with its sighting vanes is located, the alidade is moved up and down until a golden spot of light shines down through the upper sight and onto the lower sight. From the scale of degrees, the height of the sun is then read off whilst its position on the Zodiac is found by converting the day and month of the year into a position in degrees and minutes on the Zodiac. This is done using a circular conversion scale that lies inside the scale of degrees used for measuring (for more on this see Part III below). On the obverse side, the rete is set so that the sun’s position on the Ecliptic lies over the almucator that indicates its height in the sky, with morning observations being on the eastern, or left-hand side and afternoon heights on the western, right-hand side of the midday line. Using the rule, from this point, the time can then be read off on the outer scale that is engraved on the mater. This is shown in equal hours with a.m. being on the right-hand side and p.m. on the left and the numbers accordingly running clockwise from 1-12. In the case of stars the procedure is the same except that the star must be observed by looking through the sights and there is no need to convert the day of observation into a position on the Zodiac. Following observation, the star observed is located on the rete and the rete is rotated until the position of the star rete lies over the alclmucator that represents the its height. Using the rule, from this point, the time is then read off as before. By adapting these procedures, the rising and setting times of heavenly bodies can be computed for any day of the year.

On an astrolabe, unequal hours are shown by arcs that, on the empty part of the plate that lies beyond the observer’s horizon, curve from the Tropic of Cancer out towards the Tropic of Capricorn. These have their beginnings at the point where, near the centre of the plate, the vertical axis crosses the observer’s horizon. Between the two extremities of the horizon that lie either side, the arcs of the Equator and the Tropics are divided into twelve. This generates trios of points which are then joined together by the arcs of circles whose radii get larger and larger as the vertical is approached. On the diagram given by De Barbero instead of showing the Equator and Tropics, the circles for the signs of the Zodiac have been shown which results in three extra circles.

As with the hour-lines on the old quadrant, the unequal hour-lines on an astrolabe are drawn from the circles that summarise the East-West movement of the position of the sun at a given time of day over the course of the year. Where on the old quadrant, the 6 o’clock circle becomes the smallest circle and the twelve o’clock circle becomes an infinite circle whose circumference is a straight line, on an astrolabe the reverse is the case.  Apart from this reversal, the transformation is also slightly different and instead of approaching infinity exponentially, the circles of increasing radius approach it following a curve known as a tractrix.

This is because unlike on the old quadrant, where the circles that generate the hour-lines are nested and all grazing each other at a single point, have centres that are spread out along a straight line, on an astrolabe the circles are rotationally displaced so that their circumferences cross not only where the horizon meets the vertical but also at other points. This twisting causes the approach to infinity to follow a path that shows itself, not only in the increasing lengths of the radii relative to reach other but also on the plane of projection itself and when the drawn circles are examined, their centres will be found to follow a line that is itself a tractrix.

 

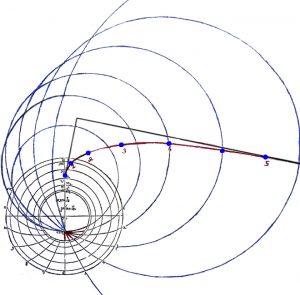
In the one direction, the approach to infinity is taken by the centres of the circles associated with the hours 1-6 as shown above, in the other, by the hours 6-12 so that although not shown above, the result is two tractrixes placed base to base.

Although on an astrolabe the hour-lines are beyond the horizon of the observer and thus show the hours of night, this is not a problem as the equal hours of day that the astrolabe shows on the other side of the horizon, can be carried across by means of the rule – either to the corresponding equal hours of night or to the lines of unequal hours. To convert the equal hours that the astrolabe computes and works with, into unequal hours, the rule is set to the position of the sun on the Ecliptic. Using the rule, the point diametrically opposite is identified and either from the unequal hour-line that cuts through it, or from the unequal hour-lines either side, the time is then either read off or inferred.

On the new, or astrolabe quadrant of Profatius, the four quarter circles of which an astrolabe as a whole is composed of are shown condensed onto a single quarter and in his Third and Fourth Books of Solar Horology, Finé describes how this is done. On a circle, B,C,D,E which has A as centre, four quarters are marked out and one quarter is divided into nine segments of 10°, with the third segment away from the vertical being divided into individual degrees so that 23.5° can be counted out and marked as point „F“.

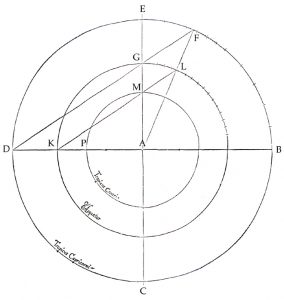
A line drawn from D to F cuts the vertical axis at point G and with A as centre, a second circle is drawn with radius A-G. This represents the circle of the Equator, enclosed within the outer circle of the Tropic of Capricorn. On the circle of the Equator, with reference to line A-F, point L is found which like E-F, is 23.5° away from G. From point K, where the Equator crosses the horizontal that bisects it, a line is drawn up to L and where it crosses the vertical is marked as point M. With A as centre and with a radius A-M a third circle is then drawn that represents the Tropic of Cancer.

In the lower right-hand quarter, beyond Capricorn, starting from the vertical axis and counting upwards, a four-tracked, serpentine scale is made that winds its way continuously from 0°-90°, 90°-180°, 180°-270° and from 270°-360°. Beyond this, a scale of 15° intervals is also marked out using the arcs of circles as on the old quadrant. This time however, the 15° intervals represent the hours of the day from 12/0 to 6, going from the horizontal down towards the vertical and then back again via 7 to return to 12. As they are derived from the hour-lines of an astrolabe, this time the markings represent equal hours.

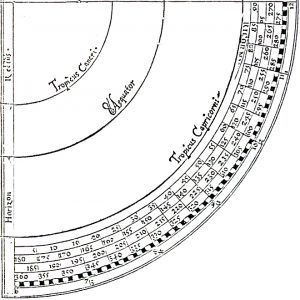
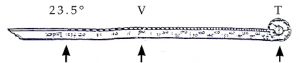
Between the arc of the Equator that lies in the quarter above the quadrant and K, lines are drawn every 5° and the points of intersection with A-G marked off. The thus established intervals are then transferred to the ruler of the instrument which, pivoting at T is mounted at A. To continue the scale beyond V, the same procedure is applied to E-F on the Tropic of Capricorn. The ruler is calibrated along both edges, once from V = 0° inwards towards T =90°, once from T = 0° out to  V = 90° and then again out from V = 0° to 23.5°.

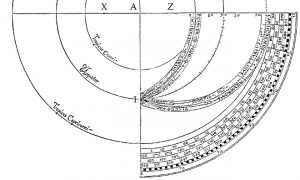
On the projection, the Ecliptic is an eccentrically placed circle with a centre either at X or at Z. Folding the projection into the space of a quarter circle, means that the two segments that extend from I to B and N must in both cases double-up and be marked with the missing information from the other quarters. This results in the spring and summer signs being shown on the smaller, inner segment whilst the autumn and winter signs are shown on the larger, outer segment, with the scale of degrees being calibrated with the ruler, mounted at A, and the serpentine scale of degrees that lies beyond Capricorn. This results in them, as on an astrolabe, being marked out as unequal intervals which cluster together where the two arcs meet at the first point of Aries.

Using the scale on the ruler that commences at T, 5° intervals are marked out along A-N-H and arcs with centres along the line D-K-P-A are drawn that pass through these intervals and through I with I-A and I-C being straight lines.

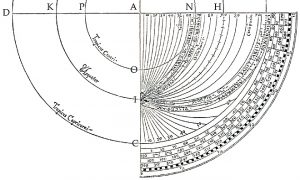
Using the ruler, from the Equator the positions of the major stars can be marked in along with the Zodiac sign of each star concerned so as to avoid confusion as to which quarter it belongs to. The user must therefore think in terms of four quarters even though there is only one.

Like the astrolabe, from the new quadrant as designed by Profatius, a variety of information can be extracted and calculated. With respect to the stars and the position of the sun relative to them, the new quadrant is universal as everything that is related to the observer is introduced via the ruler and the positions of the stars and sun as charted from the first point of Aries. Yet if all that is required is the telling of time, the positions of the stars and the lattice that spreads out from Aries can be left out, leaving only the arcs of the Tropics, the Equator and the hours of the day. To set the Latitude for a new, or astrolabe quadrant as a time-telling device, a sliding Zodiac scale must be fitted as on the old quadrant and the mid-point moved to the position on the scale of degrees that indicates the altitude of the sun on the day of the Equinoxes. To increase accuracy the arcs of the Tropics are exchanged. With 6 o’clock being represented by the vertical and 12 o’clock by the semi-circle, when the midday sun is observed, the instrument must be pointed high in the sky, while around 6 o’clock, it is aligned with points close to the horizon.

Once the semi-circle that denotes twelve o’clock has been marked out, the plumbline is pulled tight over each of the major divisions of the Zodiac so that the point where it crosses the twelve o’clock line can be marked in. From the right-angle, arcs are then drawn from these points that swing across the instrument. In the case of the Equator and the Tropics of Capricorn and Cancer, the arcs are carried over to the upper edge while the other lines are terminated at twelve o’clock. The Equator and Tropics thus marked out, the sliding scale of the Zodiac becomes surperflous as the same information is given by the arcs. Using the plumline and the scale of degrees, the sun’s altitude, derived from the analemma given above, is marked out for each hour of the day. The respective points are then joined together by the arcs of circles of increasing radius whose centres successively follow the arc of a circle that runs from the centre of the midday circle down to where the scale of degrees meets the vertical edge of the instrument. Where on the old quadrant, the hour-lines meet at the right-angle, on the new quadrant, they meet at a point a little above the right-angle and marginally inwards from an extension of the instrument’s vertical edge. Once this point has been established, further arcs can then be found with reference to the height of the sun at the Tropic of Cancer without the need for other hours to be considered. As the centres of the hour-lines get larger, their centres follow a straight line down from the centre of the 12 o’clock circle, with the direction of the straight line varying according to Latitude. At Latitudes higher than 60° North, these lines no longer depart from the centre of the 12 o’clock circle and instead move „unanchored“ downwards.

The new quadrant is used in the same way as the old quadrant with the sun’s angle of declination for the day concerned being extracted from a book of tables, the plumb-line pulled tight and the marker set at the point where the plumb-line crosses the semi-circle that marks the sixth hour. The altitude of the sun can then be measured, with the position of the marker on the plumb-line this time indicating local time as measured in equal hours.

III. THE QUADRANTS OF JOHANNES OF GMUNDEN AND REGIOMONTANUS

Johannes of Gmunden was the first Professor of Mathematics, Physics and Astronomy at the University of Vienna and wrote on the making and use of a variety of astronomical instruments. This was an important part of the task of re-connecting astronomy with observation and empirical measurement which, essential to the scientific endeavour, had been relegated to second place during the Medieval Ages. Although Johnannes of Gmunden mainly wrote on astronomical instruments and made models out of paper and wood that have not survived, a quadrant that he made has and the points at which it diverges from the instructions given in Codex Yale 24 on how a quadrant should be made, show how he was concerned with the postulating of models and the design of instruments that were a more accurate reflection of what was observed than hitherto. The quadrant made by Johannes of Gmunden is an adaption of the new quadrant and may be seen in the Kunstkammer of the Kunsthistorisches Museum in Vienna. Made in 1438, prior to making it Johannes of Gmunden had written two treatises on the quadrant.

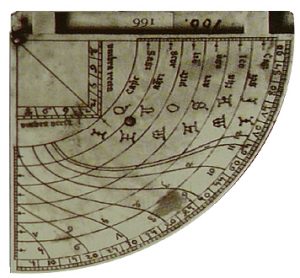
Made for Emperor Friedrich III out of ivory, the quadrant was designed for use at a Latitude that corresponds to that of Vienna and Wienerneustadt where Friedrich’s court was located. As can be seen the hour-lines are no longer the arcs of circles but have become curving „S“ shaped lines. This the result of two innovations. The first innovation is that the sun’s altitude is varied so as to reflect its movement from the Tropic of Capricorn towards the Tropic of Cancer.

The second is the division of the distance between the Tropics of Capricorn and Cancer into equally spaced intervals. From these divisions, the beginnings of the hour-lines are defined by the arcs of a series of concentric circles that have their centre in the middle of the quarter circle that marks the Tropic of Capricorn.

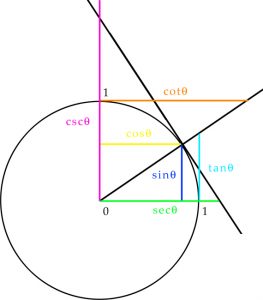
The mid-point of the quarter circle is also the corner of a device known as a shadow square. From an angular measurement of the height of a building and from the length on the ground between it and an observer, via the principle of similar triangles, the shadow square enables the vertical height of an object to be ascertained and so was common feature on quadrants and astrolabes. The shadow square is constructed by following the hour-lines on the master diagram down and across to the edge of the organum Ptolemaei, where they are projected through the central point of the containing circle back over to the lower left-hand corner, to result in a vertical umbra versa and a horizontal umbra recta.

In Codex Yale24, this information is given in tabular form on page 236: https://findit.library.yale.edu. In terms of trigonometry, the shadow square is equivalent to the tangent (tan = umbra versa) and cotangent (cot = umbra recta). On the unit circle shown below, the lower section of the hypotenuse of the larger triangle that lies between the point (sin theta, cos theta) and (1,0) is the same length as the length labelled „tan theta“ and so the whole of the hypotenuse, extended out to infinity is referred to as the tangent of the circle, with the word being used in this sense, in all cases of a straight line that grazes an arc or cirle.

On its reverse side, the quadrant made for Emperor Friedrich III features a volvelle, while the inscription, a,e,i,o,u, stands for „All Earth Is Under Österrich“ which was Friedrich’s personal motto and so identifies him as the owner of the instrument (for a more detailed image see: https//www.khm.at).

Consisting of a series concentric rings, a vovelle enables the days and months of the year to be aligned with the sun’s position on the Zodiac and combined with the phases of the moon.Working inwards from the Zodiac and calendar, two rings show the days of the lunar month, one with 28 days in a cycle, the other with 29.5. On a calendar that dates from 1460 and which was orginally made in Nuremberg but which is now in the depot of Museum Krems, a 76 period is covered using data computed by Johannes of Gmunden for the years 1476-1533. On opening the triptych, behind the figures of Saint Sebald, the patron saint of Nuremberg and Empress Kunigunde, the calendar unfolds, followed by tables and diagrams which show the Golden Numbers, Sunday Letters and the signs of moon by means of which the latter’s phases and the dates of Easter may be arrived at. Here, the lengths of the lunar months vary between 27.5 and 30.5 days with the majority being of 29.5 days in length. Meanwhile the solar year has 364 days, with an average solar month thus being 30.333 days long. With lunar months alternating between 28 and 29.5 days, over 19 years, 240 lunar months synchronise with 12 x 19 solar months, with four days left over which are inserted as leap years. Giving the impression of corroborating  the various arithmetic permutations that are possible, is the fact that as the moon rotates around the Earth, so the Earth rotates about the sun. Thus in its rotatation around the sun, the moon as a satelite of Earth, must rotate an additional amount to make up for the moving Earth. This results in the moon’s orbit around the Earth taking 27.3 days whilst its orbiting around the sun together with the Eath, takes 29.5 days, with it being this latter process that results in its phases. The endeavour of finding how these divergent totals are to be united in a cyclically repeating system constitutes the problem of the calendar and although the volvelle gives the appearance of solving these problems, this is in fact not the case and on the instrument, the sun and moon can only be synchronised through the introduction of external information drawn either from tables or from observation. The year after he made the quadrant for Friedrich III, Johannes of Gmunden compiled a much used calendar that provided the basis for the triptych owned by Museum Krems. Such calendars were also drawn up by Peuerbach and Regiomontanus with a printed example of a calendar by Regiomontanus for the years, 1474, 1494 and 1513 forming the first sixty-four pages of Codex Yale 24, with a volvelle being given on page 62: https://findit.library.yale.edu. Meanwhile on pages 37-39 there is a description of how the dates of Easter and the other moon-defined Church festivals are to be arrived at. For examples of other volvelles, along with instructions and templates for the making of one, see: https://astrolabeproject.com.

On page 63 of Codex Yale 24, a depiction of a quadrant is given by Regiomontanus at the end of his calendar for the years 1474, 1494 and 1513: https://findit.library.yale.edu. For use between Latitudes 36° to 56°, it is precisely this quadrant that was a feature of the studiolo built by Duke Frederigo di Montefelcro in the Ducal Palace in Gubbio. Here the instrument is depicted in intarsia, using wig-tree wood and is show hanging in a cabinet with an armillary sphere and some books. Meticulously restored, the studiolo is on display at the Metropolitian Museum in New York.

As Frederigo’s court astrologer was Jacob von Speyer, who corresponded with Regiomontanus, the carefully reproduced resemblence of this unusual form of quadrant is easily explained. Nevertheless it is also possible that Regiomontanus, who spent a number of years in Italy may himself have visited Urbino.

The instrument is a variation of the new quadrant with curves that derive from the gores of azimuth on the astrolabe projection used by Profatius. This takes place by reflection and inversion so that as on the old quadrant, the six o’clock hour-line is once situated again at the top.

IV. CUSANUS‘ DE DOCTRA IGNORANTI

Between 1453 and 1460 the monks at Melk followed an exchange of letters and articles known as the Controversy of the Doctrine of Ignorance in which, via the speculative theology of Cusanus, the issues raised by the tacit need of instrument-makers to resort to non-Euclidean geometry, reappear in Codex Yale 24. The Controversy of the Doctrine of Ignorance was precipitated by Vincent of Aggsbach, a monk and former prior of the Aggsbach Charterhouse which was only a few miles down river from Melk. At the Charterhouse, although all monks strove to come closer to God, there was a select group who, known as „hermits“ would live alone, only seeing fellow hermits once a week, when they ate a meal communally and afterwards were allowed to go for a walk together and talk. Today the foundations of the hermits‘ cells at Aggsbach may still be seen, enclosed by the walls of a garden with towers on which there are sundials.

The background to the Controversy of the Doctrine of Ignorance was a work that Cusanus had written in 1440. This was De doctra ignoranti, which had repeatedly prompted theologians to write replies in which they formulated their own positions and it was Vincent’s of Aggbach’s reply to one of these other tracts that initiated the controversy. In De doctra ignoranti, Cusanus developed a form of speculative theology based on the general characteristics of numbers and geometrical figures, which he then extrapolated out to the physical world and all that is and and all that exists within it. Arguing that although the infinite, all-enclosing oneness of God could not be reduced to or equated to conventional geometry, aspects of the sphere and circle could nevertheless be used to show how God transcends human rationality. For Cusanus in approaching God, it was important to realise that one knew nothing. In one of a number of geometrically derived exercises, associating that which was divine and eternal with that which was circular and that which was straight and countable with that which was mortal, he argued that any polygon, regardless of how many sides it might have, would always be different from the circle that enclosed it. Conversely should a polygon have an infinite number of sides, it would in fact be a circle and would no longer be no longer a polygon. This was because a polygon is a many-sided regular figure whose sides can always be divided by two, so that the total number is automatically doubled. With a circle this is not possible as the number of sides is already infinite and cannot be increased any further. Therefore, as soon as one says that the process of doubling can no longer be carried out, the polygon has ceased to be a polygon and has becone a circle and in becoming so, has transcended the bounds of that which is straight.

Dubbed by Pope Pius II as „the Hercules of Pope Eugenius (IV)“, Cusanus was an papal diplomat who frequently travelled on church missions and negotiated at councils. Interested in astronomy, on his travels he was always on the look out for manuscripts and astronomical instruments. On the occassion of a Reichstag held in 1444, when the Holy Roman Emperor, Friedrich III and his Electors met in Nuremberg, he recorded:

„I bought there a very large globe (showing the celestial sphere), an astrolabe and a torquetum, the book (by Ptolomy) of the Almagest and fifteen other books for 38 Rhein Gulden.“

Today all three of these artefacts can be seen at the Cusanus Hospice in Bernkastel-Kues. The torquetum is an instrument that combines a map of the heavens made as projected stereograühically from the North Pole with a second projection which shows the hour-lines and circles of ascention of an observer at another Latitude. Where the one plate is inclined with the tilt of the Ecliptic the other is inclined according to the Latitude of the observer. At the top of the instrument there is a dial and sighting-vane from which the angular height of a heavenly body may be measured and read.

In Codex Yale 24, a torquetum is discussed in an unillustrated tract by Johannes of Gmunden which begins on page 417: https://findit.library.yale.edu. Like an astrolabe, a torquetum enables the positions of the stars and sun to be ascertained. Where the astrolable solves these problems through the juxtaposition of a stereographic projection from the pole and one from the Latitude of an observer, the inclined plates of the torquetum solves these problems in three dimensions. This means that instead of different plates being required for different Latitudes, all that must be done is that the inclination of the plate that gives the observer’s hour-lines and angles of altitude must be adjusted. On Cusanus‘ astrolabe the rete is missing, allowing an un-interrupted view of the plate.

On the reverse side there is a calendar and scale of degrees showing the position of the sun in the Zodiac, a shadow square and a sighting vane. For a better image see: asstellungen.deutsche-digital-bibliothek.de

In his De doctra ignoranti, Cusanus argued that the absolute largest thing that can be, was such that it could not be in any way smaller, as then it would no longer be the largest thing that was. Likewise the smallest circle must be such that it cannot in any way be larger. As the circles are derivable through processes of infinte expansion on the one hand and infinite contraction on the other and thus involve an operation that involves the infinite, Cusanus saw the two a being necessarily related to one another in a way that dissolved space and time. In the case of an infinitely large circle, the centre is everywhere and nowhere, for the line of the circumference is infinite and straight and if the centre is at an equal distance from all points on the line, then it must in a sense be everywhere and nowhere. In the case of an infinitly small circle, the same holds true as the circle is so small that it can no longer contain the point that is its centre. Echoing the lines of unequal hours on astrolabes and quadrants, an illustration in De doctra ignoranti shows nested circles of ever increasing size in which the largest possible circle is indicated by a straight line. The essence of Cusanus‘ argument was that while the circle and sphere were capable of containing that which was straight, that which was straight could never attain the status of that which was curved. He thus used rational thought to show how, when it comes to the infinite, that which is inherently finite will always fall short of the infinite and the only way that we can intellectually grasp the nature of the infinite, is through the use of deductive reasoning that exposes the paradoxical nature of our attempts to comprehend that which cannot be comprehended. Cusanus‘ position is thus Socratic as, when it comes to God, the divine and the nature of the world as whole, like Socrates, Cusanus holds that all we really can know, is that we know nothing. This however does not mean that a rational way of looking at things cannot lead to God but rather that it peters out in dilemmas and paradoxes that dumbfound and baffle us. From this form of learned ignorance, we can then reach out towards God. Carrying his reasoning over into the physical world, Cusanus argued that the universe must infinite and that accordingly the Earth could not be at its centre. Following on from this, he deduced that there must be other life forms in the universe and that the Earth must be in motion even though we do no direct impressions of this. From the shadows cast during eclipses of the sun and moon, he knew that the Earth was larger than the moon and smaller than the sun. Thus aided and prompted by geometry and astronomy, Cusanus saw human beings as being able to contemplete the world and arrive at deductions and realisations that lead to feelings of awe and wonder and which, through the recognition of the limitations of our powers of reason could help point us towards the divine. Taken by himself, Cusanus saw man as nothing and it was only through God and his creation that answers to questions could be found and self-recognition and the beginnings of an understanding of God and the divine could be attained. Nevertheless, as something that is arrived at through the use of intellect, Cusanus‘ position was diametrically opposed to that of Vincent of Aggsbach, who denied that the intellectualised form of ignorance advocated by Cusanus could be of any assistance in the search for God. This was because Vincent of Aggsbach saw the rational as something that had to be abandoned completely and as something that was not even fit to be used as a starting point. For more on this position, see the article, Where God whiles …, on the Reloading Humanism „News and Wachau Tips“ page.

V. CUSANUS‘ DE CIRCULI QUADRATURA

After the sceptical position expounded in De doctra ignoranti, over the years Cusanus began to see that, by accepting the infinite nature of the universe and in mathematics, by postulating the infinite as something existed as a fundamental charactereistic of the world, there were ways by which, in a step by step fashion, that which was circular could be approximated to and approached. This in turn influenced his position with respect to our knowledge of God so that even before the Controversy of the Doctrine of Ignorance had started, he was already refining and developing his views on how God could be approached. Called upon to voice his opinion, with respect to the theological aspects of the controversy Cusanus draughted two replies. In addition, between 1450 and 1457, he wrote seven tracts on the squaring of the circle and how the infinite could be approached mathematically. The first of these works was De circuli quadratura in which he argued that while π was something could be approached, it could still never be precisely attained. In accordance with this view he then gave an approximation that approached the value arrived at by Archimedes in his Measurement of a Circle. Investigating a  96-sided regular polygon, Archimedes had arrived at a value for π of between 3 1/7 and 3 10/71. Yet at the beginning of his On the Sphere and the Cylinder, Archimedes had stated that where there is a straight line that extends between two points, through a process of successive division, which in the extreme case may be continued ad infinitum, any point on the line designated by another means can be reached and thus defined. This Cusanus realised, was only true of intervals that were defined by straight lines and did not include intervals that were in any way derived from curves. Although with reference to a point, other points on a straight line can be defined by means of an arc that, with a centre at some point on the line, is then swung across the line, at the point where the arc crosses the line, the arc is seen in terms of a tangent and at this single point, the tangent is perpendicular to the line it crosses. Yet in all other cases of arcs that intersect, either with each other or with straight lines, although the results look angular, Euclidian geometry denies that they are angles. Here, the two examples that involve straight lines are related to the sides of a polygon contained within a circle when the number of sides is progressively increased, for as the process continues, the cut-off left-overs between the polygon and the circle become progressively smaller and with them, the cornicular angles that pertain between the sides of the polygon and the circumference of the circle. In this way the polygon approaches the circle but can never reach it, as for any polygon defined or constructed there will always be one with a greater number of sides and thus with cornicular angles that are smaller than those generated by the preceding polygon. The situation is thus related to the unequal hour-lines an old quadrant which, as angular extents from six o’clock to midday are marked out, describe the arcs of circles that grow ever larger until at 90° a circle of infinite radius is reached. In both cases one is reaching out towards a form of infinite that transcends that of straight lines and Cusanus realised that in the case of a polygon, the cornicular angles associated with any approximation to a circle were equivalent to the numerical amount by which the value for π arrived at using Archimedes‘ method differed from the actual value. Although these cornicular angles cannot be quantified, they are however real and in any approximation, the reduction in angle is an indication that a closer approximation has been arrived at. Just as the polygon can never become a circle without ceasing to be a polygon, so any approximation to π will always be constrained by the logic of straight lines and so can never acquire the crucial aspect of that which is circular.

In the case of a circle of infinite radius, however infinite the radius is, the circumference will always be 2π times longer, with the elusive nature of  π further meaning that the exact amount can never be arrived at. This means that not even a straight line of infinite extent can encompass that which is circular bur rather that which is circular will always enclose that which is straight. In mathematics Cusanus was the first person to realise that π is neither a rational number, nor is it an irrational number but rather, is what mathematicians now call a „transcendental number“. This means that there is no quadratic equation in terms of which the transcendental number can be expressed in a way that the elements of the equation can be arranged so as to make zero. Thus although the root of two is an irrational number, it is the only number that satisfies the equation: x² − 2 = 0 and accordingly root two is not a transcendental number. Likewise, the equation x2 − x − 1 = 0 represents the number phi, which is associated with the Golden Section and which whilst irrational, is not transcendental. Like the square, when the sides of other polygons are assigned lengths that are characterised by rational numbers, their diagonals are either rational or irrational and so can be expressed by means of a quaratic equation. In the theoretical case of a polygon that becomes a circle, a transition takes place and the numbers characterising the polygon also change and ceasing to be either rational or irrational numbers become instead transcendental. As the name suggests and as the squaring operation that it contains implies, quadratic equations are associated with all that is linear, while transcendental numbers are associated with something else. In the case of π, this something else is rotational and is that which enables the radius of a circle, despite being straight, to sweep out angular motion and so describe a circle. Angular motion thus generates something that escapes the net cast by a quadratic equation. As Cusanus saw, associated with both irrational and transcendental numbers are differences known as „infinitesimal’s“. This is because between any enumeration of an irrational or transcendental number and its approximation, there is a difference that as the accuracy of the approximation increases becomes infinitesimal. In the case of a circle and a polygon, as seen, the unquantifiable cornicular angles are equilvalent to the infinitesimal differences between an approximation to π and the actual value. Infintessimals were first discovered by Zeno of Elea who found them so contradictory that he used their existence to argue that change and movement in the universe were impossible. Infinitesimal’s involve acknowledging that between any two points on a line or between any two numbers in a series, an infinite number of divisions can be made. This suggests that on such a line, any irrational or transcendental number can be arrived at simply by dividing the line often enough. While this true of irrational numbers, as Cusanus knew, despite the infinite amounts of division that may be invoked, this is not true of transcendental numbers which are a different species of number. Following the discovery and acceptance of irrational numbers, the infinitesimal’s that are associated with them were seen with suspicion as there was reluctance to postulate that the universe was inherently infinite. Yet Cusanus saw things differently and argued that the infinite nature of the universe was a reflection of the infinite nature of God and accordingly saw each improved approximation of π as an approach towards a facet of God.

Having established the unreachable and yet approachable nature of π, in De circuli quadratura, Cusanus considered an equilateral triangle together with two circles, one which it encloses and one which it is enclosed by. As the radius of the smaller circle is half that of the larger and as the smaller circle has a radius that is rational, it follows that both circles have radii that are rational. It also follows that between them there will be a circle whose circumference is exactly that of the perimeter of the triangle. The question is then of whether the radius of this third circle is rational/irrational or transcendental. Although transcendental, Cusanus shows  how it may nevertheless be approached.

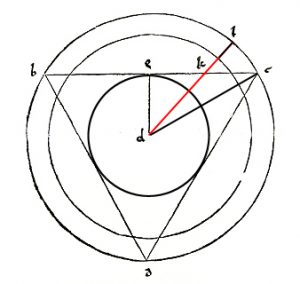
To this effect, line b,c a quarter of the way in from c. This results in point k. If from the centre of the two circles, d, a line is drawn from b to k and if d,k is then extended by a quarter, the result is a circle with a circumference that is equal to the perimiter of the triangle.

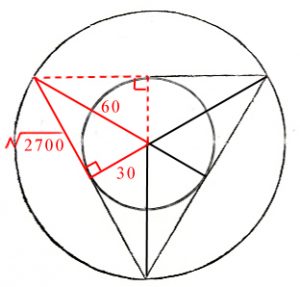
Following the method used by Archimedes in his approximation to π , the radius of the enclosing and enclosed circles associated with any polygon are related to one another by a right-angled triangle which is formed from their radii. The two radii give the lengths of the shorter side and the hypotenuse and this enables the remaining length to be arrived at using Pythagoras‘ Theorem. The length of the side of the polygon concerned is then obtained when this length is multiplied by two. In the case of an equilateral triangle, if the radius of the enclosing circle is said to be 60 then that of the enclosed circle is 30 and this means that the longer side is √2700 in length. Inside the equilateral triangle, this 30,60,√2700 triangle, reflected about itself six times, forms the equilateral triangle. Half of √2700 is √675 and this indicates the quarter point on the side of the equilateral triangle. Meanwhile the distance from the centre of the circle to the quarter point is √1575.

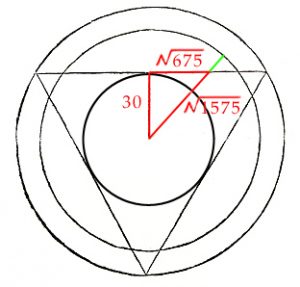
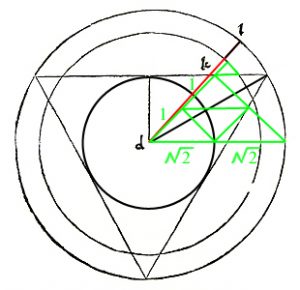
As the circumferance of a circle is given by the formular 2πr, π is found by dividing circumferance by diameter. As the circumferance is the same as the perimeter of the equilateral triangle and this is 6 x √2700, dividing this by 2 x 5/4 x √1575 results in a value for π of 3.1423376 which is an improvement on the approximation given by Archimedes of between 3.1428571 and 3.140845. That the method is an approximation can be seen by the fact that when a radius of exactly 2 1/2 is constructed using 1,1√2 triangles it emerges that it does not pass through k but through a point slightly beyond k.

VI. CUSANUS‘ QUADRATURA CIRCULI

The presence of Cusanus‘ next tract on the squaring of the circle among the manuscripts of Yale 24 is significant as it shows that in the Controversy of the Doctrine of Ignorance, the monks at Melk were following the debate not just theologically but also mathematically. Entitled Quadratura circuli, this work also appears to date from 1450 with the Yale version on pages 449-454 being one of only two manuscript copies to have survived: https://findit.library.yale.edu.

Where in the first part of De circuli quadratura Cusanus had argued deductively to establish that π was transcendental and had then given a specific method by which it could be approximated to, in Quadratura circuli he established the transcendental nature of π geometrically and then went on to give a generalised and likewise geometrical method by which margins could be identified within which π lay. Unlike the specific method given in De circuli quadratura, the „geometry of the infinite“ of Quadratura circuli, allows ever-improved approximations to be made. Cusanus first considers a line, a,b, from which an equilateral triangle is constructed whose sides are formed from a,b in a such way such that nothing is left left over. He then constructs a square whose sides, in like manner, are a,b divided into four. Comparing the two figures, as in De circuli quadratura he observes that in both cases and indeed in any regular polygon, in addition to an enclosing circle and an enclosed circle, there is also a third circle whose circumference is equal to the perimeter of the polygon.

As regular polygons acquire ever more sides, so both the enclosed and the enclosing circles approach the dimensions of this third circle and these piecemeal steps towards the third circle, are real steps even though the circle itself can never be attained. Considering the triangle, Cusanus observes that if the radius of the containing circle is 14, then that of the contained circle is 7. Seven is also the mean between 0 and 14 and on the diagram above is taken as the length of f,n and h,t, while aa,p and t,o are given by the differences between the two circles associated the triangle and the two circles associated with the square. These result in triangles g,aa,p and h,t,o which are then enlarged to form triangles g,bb,q and h,s,q with q designating the radius of the circle whose circumference is that of the line a,b. As this is however hypothetical, the triangle g,bb,q is in fact triangle g,bb,u with there being a gap between q and u with q giving the upper limit and u giving the lower limit. That g,pq and b,t,q and thus also g,p,u and h,t,q, are straight lines reflects the fact that Cusanus sees the progression towards the sought circle as being linear with relations between analogous parts being characterised by a single proportion.

At the beginning of his Measurement of a Circle, Archimedes had stated that the area of a circle is equal to that of a right-angled triangle whose height is the radius of the circle and whose width is the circumference of the circle. Adapting this by saying that the area of a circle is equal to a rectangle formed by the radius of the circle and half the circumference, Cusanus develops a diagram which shows that, given the radius of a circle, everything else that one wants to know is related to π which however is unknowable.

In the diagram, the circle on the left-hand side has a radius of length 1 and the rectangle formed from it has of length π, so that the area of the rectangle is the area of the circle. If the side of the rectangle of length π is extended by 1 and the resulting lenth is divided in half, using this new division as a centre, the semi-circle shown above may be drawn. This has a length that is equal to the circumference of the original circle. The right-hand side of the rectangle is then extended up as far as the semi-circle. Using this new length, a square can be constructed that, with sides of √π, squares the original circle.

Although π is unknowable, as in De circuli quadratura, Cusanus supplies a rule of thumb by which the process of aproximation can be initiated. This is the ratio 16:9 which relates the lengths of r,q to s,u and s,u to to r,s and r,s to a,b. As the radii of the containing and contained circles of the equilateral triangle are 7 and 14 then it it follows that the half-lengths of its sides are √147. This multiplied by 9/16 makes √(82 11/16) which is both the length of the half side of the square and the radius of the contained circle. Again using Pythagoras‘ Theorem, the root of twice this amount, in other words, √(165 6/16), gives the square’s diagonal and the radius of the circle that contains the square.

If from √(82 11/16) 7 is subtracted this gives the difference between of the radius of the circle enclosed in the square and the radius of the circle enclosed in the triangle which is a difference of, as Cusanus says, „a little bit more than two“ (9.093 – 7 = 2.093). If from 49, √(165 6/16) is subtracted, the difference of „a little more than one“ (14 – 12.86 = 1.14) will be arrived at between the radius of the circle enclosing the triangle and the radius of the circle that encloses the square. On the first of the three diagrams above, these form aa,p and t,o and if the lines of the hypotenuses of g,p and h,o are extended out towards s,r, they will approach q. This is done duplicating the triangles g,aa,p and h,t,o and attaching them to the original triangles so that the lines of the hypotenuses are continued. This results in triangles g.bb,q and h,s,q. The new radii are then found by adding 2.093 to 9.09 which makes 11.186 and subtracting 1.14 from 12.86 which leaves 11.72. As the circumference of the circle is the same as the perimeters of the equilateral triangle and the square which are 6 x √147 and 8 x √(82 11/16) which both make 72.746, this figure, divided by the two diameters obtained specifies the bounds within which π lies. This is because the extended triangles have fallen short and do not meet at a single value. Where 11.72 gives a value of 3.1034, 12.86 gives a value of 2.828 and this results in a  range which is wider than that given by Archimedes. To improve upon this, the triangles are again duplicated and then reduced prior to the lines of their hypotenuses being extended as before. As it is only the height of the triangles that is of interest, this is achieved by taking the difference between 11.186 and 11.72 and multiplying it first by 2.093/(1.14 + 2.093) and then by 1.14/(1.14 + 2.093) to result in intervals of 0.345 and 0.188 which respectively are added onto 11.186 and subtracted from 11.72 to result in 11.532 and 11.531. The circumference of the circle is then divided by two times the mean radius to result in a value for π of 3.154. Although this lies outside the range established by Archimedes, Cusanus‘ primary purpose was to establish from first principles, a general method by which ever improved results could then be generated. This he saw as being possible through the application of the same technique to polygons with more sides that the equilateral triangle and the square. In this way, Cusanus saw the regular plane figures as pointing towards the divine transcendence of a circle even though they could not attain it.

The relevance of Cusanus‘ mathematics to his theology was that in astronomy, what mathematicians call „chords“ were the basis of the mathematics used by Ptolemy in his Almagest. This was because trigonometry at that time, although it did exist, was still very much under development and Ptolemy choose instead to draw on the well-established and codified tradition of Greek geometry. A chord is a straight line drawn within a circle between any two points on the circumference, with the side of a regular polygon contained in a circle being an example. Using a circle of radius 60 and departing from the examples given by Euclid in his Elements, Ptolemy used Pythagoras‘ Theorem to calculate the values of the 360 chords that lie opposite every 1/2° of arc from 0° to 180°. These he then gave in Book I of his Almagest as the basis for all else that followed. Like Ptolemy, Regiomontanus used both chords and degrees of arc so that during the Renaissance, chords were still very much associated with astronomy and this explains the presence of Cusanus‘ tract in a volume of works dedicated to astronomy and the calendar. Cusanus‘ use of the sides of regular figures as ways by which π and thus God could be legitimately approached, thus made astronomy and the mathematics that was associated with it, in like manner reach out towards God, so that from the initially highly sceptical position of De doctra ignoranti, Cusanus can be seen as moving over to a more conventional form of Neo-Platonism. This in turn suggests that over the years, he will have seen the copy of Ptolemy’s Almagest, along with the torquetum, the astrolabe and the globe of the celestiel sphere that he had acquired in Nuremberg in 1444, in a new light. Instead of representing an end-point of knowledge, they will have slowly come to stand for the starting point of a new kind of knowledge.

On page 454, the Yale manuscript of Quadratura circuli includes a figure that does not occur in the principo precepts. This is equivalent to the left-hand diagram above: https://findit.library.yale.edu. For the reader, the production of such diagrams is part and parcel of understanding a Renaissance text on geometry, as steps are frequently left out and there is often much that is not explained. This the reader is left to work out and think through. While this makes for slow reading, once an issue has been grasped, there is a deeper understanding that is not easily forgotten. It also underscores the Renaissance view of the world as a labyrinth that one must be read and work one’s way through. For more on this, see the article, The World’s a Labyrinth! on the „News and Wachau Tips“ page.

VII. PEUERBACH, REGIOMONTANUS AND CUSANUS

A student of Johannes of Gmunden, even before he had graduated, Peuerbach was invited to give a series of lectures on astronomy at the University of Padua which was held in 1449/1450. In Italy, Peuerbach encountered humanism and met Cusanus with whom he stayed for some months in Rome in 1451. He then returned to Vienna and completed his studies in 1453. Thereafter he taught classics at the University of Vienna and astronomy at the School of Saint Stephen’s. In 1453 Cusanus refined and brought together his thoughts on the squaring of circles and released De mathematicis complimentis which begins with the method of squaring a circle expounded in Quadratura circuli.  To this the doctor and astronomer, Paolo dal Pozzo Toscanelli (1397-1482), wrote a critique a copy of which he gave to Peuerbach. When in 1457 Cusanus released Dialogus de circuli quadratura, he again sent a copy to Peuerbach. Not sure of the significance of what Cusanus was getting at, Peuerbach draughted some comments and then left the matter at that. When in 1461 Peuerbach died, his papers, including Quadratura circuli, Toscanelli’s critique and the later dialogue by Cusanus were passed on to Regiomontanus. Soon after, the young astronomer recieved another tract by Cusanus. This was De una recti curvique mensura, a copy of which Cusanus had sent to the exiled Greek cardinal and archbishop, Bessarion (1403-1472). Cusanus and Bessarion had been friends since 1437, when Cusanus had travelled to Constantinople as a papal diplomat and had then journeyed back to Italy the following year, in company with Bessarion. Following Peuerbach’s death, Bessarion adopted Peuerbach’s star pupil as a protegé and so passed the text of De una recti curvique mensura on to Regiomontanus.

In De una recti curvique mensura, instead of squaring the circle directly, Cusanus gives three rule of thumb methods by which the curved arcs of a circle could be translated into straight lines of the same length and one method by which the area defined by a half circle could be translated into one defined by a rectangle. Meanwhile, as the name implies, in Dialogus de circuli quadratura, he refers indirectly to De circuli quadratura and once again considers an equilateral triangle whose perimeter is rational and which is enclosed by a circle, within which there is second circle whose circumference is the same length as the perimeter of the triangle and so is also rational. The question of De circuli quadratura is thus reversed and instead of going from the triangle’s enclosed and enclosing circles to a circle with a circumference the same length as the perimeter of the equilateral triangle, Cusanus goes from this circle, to the circle that encloses the triangle. As the circumferance of the first circle is rational, the questiion is then of whether this second circumferance is rational/irrational or transcendental. Establishing that, as before, although it is transcendental in length, this can nevertheless be approached, he then used a different rule of thumb to arrive at an approximation. Drawing a quarter of a square enclosed within the inner circle, Cusanus says that the length of the hypotenuse of the resulting triangle, a,b,c, added to one of the shorter sides approximates to the diameter, g,f, of the larger circle that encloses the equilateral triangle.

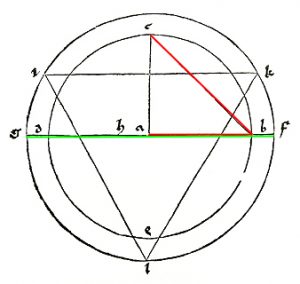
In this way Cusanus again made his point that π is something that can be approached but never exactly established. In Receiving De una recti curvique mensura from Bessarion, Dialogus de circuli quadratura together with Toscanelli’s critique from Peuerbach and Quadratura circuli from an unkown source, it was only in Venice in 1463, that Regiomontanus finally got around to formulating a response to Cusanus‘ work. Where Toscanelli had simply called into question Cusanus‘ assumption that as polygons acquire ever more sides, they approach the circularity of a circle in a linear fashion, Regiomontanus methodically established that this was not the case. When the lengths of the sides of regular figures are divided by the diameter of the circle that contains them and the changing proportions are plotted on a graph it will be found that they approach the circularity of a circle in a manner that approximates very closely to a tractrix, with the black line on the graph below being the lower part of the tractrix.

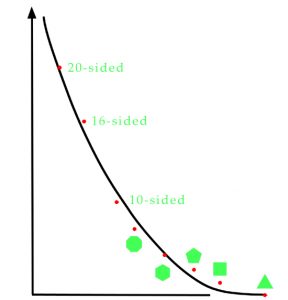
Although the tractrix was not discovered until 1670, during the Renaissance, someone who does appear to have known of the non-linear approach was Luca Pacioli who, without saying how, in his Divina Proportione of 1494/1509 declared that the Golden Ratio was the cause of all things. From the text it is nevertheless clear that this is to be understood as taking place within a circle or sphere, which then contains all the things generated. Here it would seem that Pacioli was aware of the fact that if the radius and diameter of a circle are repeatedly divided by the Golden Section, approximations to the sides of the regular figures contained within the circle will result. Due to the fact that phi = (1 + √5)/2, in the case of figures whose number of sides are a derivatives of five, the lengths arrived at are not approximate but exact.

In a painting by Jacopo de‘ Barberi that shows Pacioli together with a pupil, in addition to the composition of the painting being based on the Golden Section, Renzo Baldasso and John Logan have found that there are references to both the ratio and the number phi along with its successive powers. The relevance of this is that if the radius and diameter of a circle are divided by phi and its successive powers, every second term of the results obtained through a repeated dividing by phi will be arrived at.

Taking the increasing powers of phi and using them to create a sine wave whose wavelength increases by a power of phi every half wavelength while the amplitude is an inverse of this, provides another way of observing the increasing numbers of sides of regular plane figures as they approach a circle, with the resulting values approximately following the curve of a tractrix (for the original discussion in which a sine curve is adapted using powers of phi and its inverse see: mathstackexchange.com.)

Considering the regular plane figures in relation to the tractrix shows how, in their different ways, both Cusanus and Pacioli were on the right track. Nevertheless, during the Renaissance, as it was not known in what direction Cusanus‘ infintessimal mathematics was leading, it was his faulty mathematics that was focused on. In Quadratura circuli, had Cusanus applied his method to polygons other than the equilateral triangle and the square, he would have obtained different and less favourable results. Thus where Peuerbach was puzzled and at a loss to see what his friend was getting at, in a letter to the mathematician Christian Roder, Regiomontanus described Cusanus‘ geometry as „ridiculous“ and dismissed him as an „ape of Archimedes“. While it is correct that Cusanus did make a false assumption, for all his mathematical brilliance, Regiomontanus failed to grasp not one but three essential points. On the one hand, two hundred years ahead of his time, Cusanus was feeling his way towards the differencial calculus that would later be developed by Leibnitz and Newton. Here, between incremental values which specify a required degree of accuracy, curves are reduced to straight lines. On the other hand, a full four hundred years ahead of his time, Cusanus had realised that π was a transcendental number that was to be seen as standing apart from the traditional categories of rational and irrational. In working his way towards these realisations, Cusanus, again four hundred years ahead of his time, further called into question the basic assumptions of Euclidean geometry. It is thus ironic that when Regiomontanus‘ De triangulis omnimodis was published posthumously in 1533 by Johannes Schoner, the motif for the frontispiece was the first of the three diagrams given above from Cusanus‘ Quadratura circuli. This tract, together with Dialogus de circuli quadratura and De una recti curvique mensura, Schoner had included as an appendix to De triangulis omnimodis along with Toscanelli’s critique, Peuerbach’s notes and Regiomontanus‘ replies.

VIII. NON-EUCLIDEAN GEOMETRY AND THE REGIOMONTANUS DIAL

Following Euclid, an angle is an extent that is formed by the intersection of two straight lines with angle-like extents brought into being by the intersection of arcs and straight lines and arcs, not being seen as angles:

Thus the hour-lines on quadrants and astrolabes along with the gores of azimuth on astrolabes, although they mark out angle-like extents are denied any form of angular status and so they and what they represent, are strictly speaking unreal and devoid of application. Nevertheless they are used and this calls into question the consistency of Euclidean geometry, for how can something be used if it is not in some way real? Countering this objection, it is argued that in such cases, the angle-like extents are only used in an „as-if“ fashion that no one really believes in. Yet this is entirely analogous to the disclaimer inserted into Copernicus‘ De revolutionibus of 1543, in which it was pointed out that, although the mathematics used in the work implied that the Earth rotated around the sun, this was not actually the case. In this fashion, despite the use of angle-like extents in astronomic instruments, for thousands of years Euclidean geometry was considered to be the only form of geometry capable of describing the world. Yet the intertwined and mutually dependent nature of Euclidean and non-Euclidean geometry is shown by the fact that it is possible to derive the hour-lines on a quadrant directly from an elevation of the Celestial Sphere without invoking the circles that are associted with the seasonal variations of the sun’s position at any given time of day. This is done by taking the great circle that on an elevation of a sphere with lines of Longitude appears as a circle and reducing it by half, placing it both sides of the y-axis. Then, working inwards from one great circle to the next, the opposing pairs of elipses on the diagram below (indicated by thick lines on one side of the y-axis and by thin lines on the other), are taken and reconstructed as undistorted circles of progressively ever increasing radii. This ends when the end-on view of the great circle that lies on the y-axis is extruded out to infinity, so that it represents a circle of infinite radius whose circumference is so all encompassing that its curvature is imperceptible.

The transformation also works when from out of the great circles, spheres of ever increasing size are made. Unlike a circle, which has a curvature of +1, an inverted circle has a curvature of -1 and where a circle is enclosed within the plane in which it has been drawn, an inverted circle encloses its plane and it is this that is enclosed within the great circle that is reduced by half. In the case of an inverted sphere the same holds true and the enclosed space which once enclosed the sphere is now enclosed within a doughnut shape, whilst all around it there is what mathematicians call a surface of constant negative curvature circle. As the name says, a surface of constant negative curvature is a surface with poles and an equator, that although they exist, are never encountered as they are always infinitely far away. This means that although the surface can be envisaged as the rooves of two big tops put edge to edge this is a distortion to which the above diagram and construction exercise provides a useful corrective.

In the  „Poincaré disc model“ the above transformtation is used as a departure point for ways in which surfaces in non-Euclidean space are investigated.

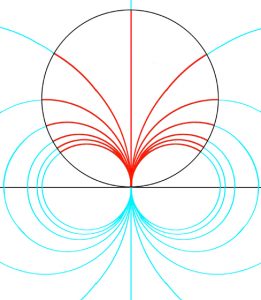
Here a boundary circle shown in black defines and encloses the area of investigation. On the model, the properties of the space being examined is ascertained with reference to the lines shown in red, while the turquoise lines are the lines of construction from which the red lines derive, with the initial two circles of the two halves not necessarily having to be the same size. Inherent in astrolabes and quadrants, the above construction shows that there is something non-Euclidean going on.

In the diagram the boundary circle compresses the infinite extent of the surface of constant negative curvature into a circle. When circular fragments from within the boundary are taken, regardless of where they were taken from, they will always result in saddle-like, potato crisp shapes of the same size that are curved in two directions.

As a whole, the figure thus represented cannot be accurately exported into conventional three-dimensional space, nevertheless, like the rooves of two big tops put rim to rim, an approximation is possible and results in what is known as a pseudo-sphere. This is nothing other than the two tractrixes that lie behind the lines of unequal hours on an astrolabe, rotated through 360°.

As seen, as regular plane figures acquire more and more sides and approximate ever more to the circularity of a circle, their sides divided by the diameter of the containing circle mark out a curve that is very close to a tractrix and as the tractrix derives from a surface of constant negative curvature and itself has a constant negative curvature, it has something inherently spherical and circular about it which the regular plane figures can be seen as approaching as they acquire more and more sides. This and the consideration chords shows how ultimately, mathematics, astronomy and the infinite are inter-related and spill over into theology, with Cusanus being the first to examine these interrelations.

Whilst Regiomontanus‘ work on spherical trigonometry, along with his replies to Cusanus‘ methods of finding approximations to π, temporarily countered the latter’s questioning the fundamental assumptions of Euclidean geometry, there still remained the fact that the hour-lines on quadrants and astrolabes used angle-like extents that Euclidean geometry denied were angles. It is possible that Regiomontanus responded to this by adapting a dial known as the navicula de Venetiis, or „the little ship of Venice“. This has straight hour-lines and straight hour-lines are also a feature of the Regiomontanus dial.

In Codex Yale 24, the Regiomontanus dial is shown on page 64 at the end of the calendar drawn up by the astronomer for the years 1475, 1498 and 1513: https://findit.library.yale.edu. Where in the drawing given by Regiomontanus the parallels of Latitude extend from 39° to 57°, in the later drawing given by Finé, they extend from 0° to 90°.

Here it can be seen how, as one approaches the point of the inverted triangle, the amount of correction that is necessary descreases, until at the equator, no corrections are necessary as there are no seasons and day and night are always of equal length. On the Regiomontanus dial, this point of the triangle is equivalent to the pinched-together, curved horn of curves at the top of a quadrant and hints at the fact that although Regiomontanus again won the battle he was ultimately fated to lose the war. For as the surfaces of non-Euclidean spaces are warped, parallel lines do meet and curved lines are able to form angles, either with other curved lines, or with straight lines. The warping of such a space means that instead of its axses being being straight, they are curved and this in a way that is the opposite to that of a circle. These considerations thus lead back to the notion of a surface of constant negative curvature. As seen, where the circle and sphere are enclosed in the planes in which they are embedded, a surface of constant negative curvature encloses the planes with which it is associated. It is thus all-enclosing and elusive in a way that is a perfect expression of what Cusanus saw as being true of the largest (and smallest) possible circle and the largest (and smallest) possible sphere. In this way, „the ape of Archimedes“ can be seen as being vindicated, with Cusanus‘ arguments in speculative theology suddenly acquiring a renewed validity and providing a symbol of that which lies beyond.

IX. PEUERBACH AND REGIOMONTANUS

Not withstanding the fact that he served as court astrologer to King Ladislaus Posthumus of Bohemia and Hungary, Peuerbach saw the heavens and all that was therein contained as the manifestation of a system that was subject to physical laws that could be rationally formulated. He was thus saw comets as physial phenomena and rejected the view that they were portents of divine origin. In a report he wrote for Ladislaus on the comet of 1456 (now known as Halley’s Comet), he identified nine differet kinds of comet. A copy of the report is held by the monastery at Melk, while in Codex Yale 24, an illustration on page 201 shows the nine different kinds of comet: https://findit.library.yale.edu. A year later, in the same year that Cusanus released Dialogus de circuli quadratura, as a part of the program of revising and checking over the ptolomaic account of planetary motion, together with Regiomontanus, Peuerbach observed an eclipse of the moon at Melk. The circustances of his being in Melk was the hospitality afforded by the monastery to King Ladislaus and his retinue as they journeyed from Mariazell to Prague where the king was due to be betrothed. As Peuerbach was Ladilaus‘ astronomical/astrological advisor, his presence at such an eventful time is to be expected. Although the royal visit and King Ladislaus‘ unexplained death soon after, ferature in the Melk chronicles, the presence of the astronomers left no trace. Evidence of the event however is provided by the meticulous records maintained by Regiomontanus of all the observations he made along with attendenant calculations and here, Melk is explicitly cited as the place of observation. These were discovered among Regiomontanus‘ papers by Schöner and published in 1544. In the chronological list of observations the Melk observation of 1457 is the first entry. Made on the Third of September, the astronomers may well have carried out their observetaions from one of two Medieval/Renaissance towers that survived the later Baroque rebuilding of the monastery.

Reconstructing the event, the astro-historian, Georg Zotti has confirmed that the data given by Schöner is completely in accord with Melk being the place of observation. Although it is not known what kind of instrument was used, an astrolabe is a distinct possibility and in the German edition of Hartmann Schedel’s Liber chronicarum of 1493 Regiomontanus is shown holding an astrolabe.

Eclipses of the moon are important for astronomers as they provide an exact alignment of sun, moon and Earth, so that from the time between two lunar eclipses, a very precise average may be obtained of the length of a lunar month. By the Renaissance it was becoming clear to mathematicians and astronomers that a calendar reform was necessary and this made the precise duration of a month one of a number of matters that were of pressing importance. In order to measure the duration of the event, Peuerbach and Regiomontanus measured the height of Alkione, which is one of the stars in the Pleiades. From the duration the event, they then extracted an exact time for the actual alignment.

As the Baroque mathematician and astronomer, Georg Matthias Bose, observed in Vienna at a celebratory speech made on the 300th anniversary of the event, Peuerbach and Regiomontanus‘ measuring the height of Alkione was the first time since Antiquity that astronomers had used time as a means of pin-pointing an eclipse and the significance of the event lay in their using the observed time as a means of critically verifying the data given in tables. Drawing from the work of earlier Islamic astronomers and from a team of Jewish scholars that Alfonso X of Castile had assembled  around him in Toledo, a book of tables giving the positions of the sun, moon and other planets was complied. Known as the Alfonsine Tables, an edito precepts appeared in 1483. Nevertheless both this work and the Almagest, the catalogue of stars and planets along with their positions that had been drawn up by Ptolomy, diverged from what was observed when precise observations were made. This was due to  the „Procession of the Equinoxes“ a phenomenna which results in the so-called „fixed stars“ appearing to rotate through 360° over a period of 25,800 years. Although this was not understood at the time, when the results of observations were critically compared with what was given in the tables, divergences were discernable. In 1460, three years after the Melk observation, Peuerbach and Regiomontanus observed another lunar eclipse, again measuring the height of a star in order to ascertain the time of occultation. Although the time of the event lay within the bounds of acceptable accuracy, the locations given in the tables were at odds with what was observed and for Bose, the Melk observations were the beginnings of a new era:

„The lover of Astronomy, who in general is not completely ignorant of her history, will immediately agree that that this already well-described lunar eclipse is the beginning of a new epoch and blooming in Astronomy. Behold! The light that this eclipse has unveiled can never be honoured and emphasised enough. The light that had been driven away by the darkness into which had Astronomy fallen, now shines like the golden red of dawn with her pink hair, in the next instant ready to announce the rising sun of Apollo. This was achieved by GEORGIUS PEUERBACH who alone carried the light back up to the heavens.“ 

In astronomy, Peuerbach’s achievement was, with respect to the motions of the planets, to significantly improve upon the ptolemaic system by shifting the points about which the planets and their epi-cycles rotated. Although he was not the first to do this, Peuerbach expounded his views with unprecedented clarity and made no bones about the fact that the ptolomaic system needed improving upon. He thus paved the way for the seminal moment when Copernicus realised that the different centres of rotation of the various planets could be reduced back to a single point and the notion of epi-cycles rendered unnecessary if the Earth was made to rotate about the sun and not the other way around.

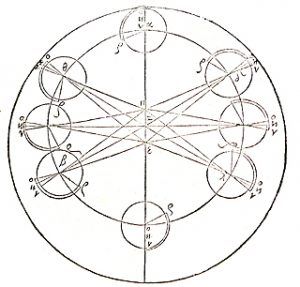
The planet Mars with its eccentric circle of orbit and its epicycles

In Codex Yale 24, Peuerbach‘ Theoricae novae planetarum, complete with coloured illustrations, features prominently at the beginning of the volume and is placed immediately after the list of contents and a printed calendar by Regiomontanuson page 65: https://findit.library.yale.edu. Introduced at the beginning of the work as „a celebrated astronomer“ a further indication of Peuerbach’s standing, both during his lifetime and thereafter, is given by the fact that his New Theories of Planets was used by astronomers up until the middle of the seventeenth century and between 1472 and 1563 fifty-six editions were printed.

An astrolabe which bears the date 1457 and which is reputed to have been made by Peuerbach, features a volvelle calendar on the reverse that is reminiscent of the one made by Johannes of Gmunden made for Friedrich III. The difference is that instead of 28 and 29.5 days per lunar cycle the Peuerbach astrolabe has lunar cycles of 28 and 30 days.

In between the solar and lunar components of the volvelle there is a shadow-square shown as a half octagon. Now held by the German National Museum in Nuremberg, in the small town of Peuerbach in Upper Austria, where is Georg Aunpekh was born, a large-scale copy of the obverse side of this astrolabe adorns the gable of the town hall while inside there is a museum dedicated to the astronomer and his life.

Meanwhile, in Codex Yale 24 there is a copy of an unillustrated treatise on the construction of astrolabes written by Peuerbach which begins at page 221: https://findit.library.yale.edu.

A tract written by Regiomontanus on astrolabes is held at the National Library in Vienna as a part of Codex Vienna 5292 and this also includes Canones albionis, a tract written by him in 1455 on the use of an instrument known as an albion. In terms of projection, the albion is similar to an astrolabe, nevertheless where the astrolabe performs calculations relating to the sun and stars, the albion is concerned with the positions of planets. In Codex Yale 24 the second tract by Johannes of Gmunden is Composito et usus cuiusdam instrumenti ad faciliter et breviter invenienda varia loca omnium planetarum. This is an unillustrated tract, which beginning on page 318 covers a form of equitorial dial that was discussed by Campanus of Novara (around 1220-1296) which is a fore-runner of the albion: https://findit.library.yale.edu. Originally invented by Richard of Wallingford during the Middle Ages, the only known example of an albion was made in Vienna sometime between 1450 and 1460.

On its reverse side, the Rome albion features a chart of the heavens based on the stereographic system of projection such as was used on astrolabes (see X below).

Although it is tempting to think that it might be possible to definitively demonstrate that this albion reflects the revised accounts of planetary motion that Peuerbach was developing at the time, Emmanuel Poulle observers that in proceeding from Peuerbach’s expositions to a physical instrument, despite the clarity of Peuerbach’s account and models, there are too many open-ended questions for any definite answer to be arrived at. Nevertheless manuscripts in Vienna such as that written by Regiomontanus do point to the albion as something with which instrument-makers in Vienna were concerned with. In Codex Vienna 2332, on folios 25 and 33 there are drawings of planetary orbits as would be engraved onto the face of an albion. Nevertheless for Poulle, the making an albion that reflected Peuerbach’s new account of planetary motion, although striven for, was something that never seen through to completion.

X. REGIOMONTANUS AND BESSARION

A year after the observations of 1460, Bessarion, appeared at the court of Friedrich III in Vienna. There he hoped to pursuade the Emperor to join him in petioning the Pope to lauch a crusade against the Turks. Although unsuccessful in mobilising help for the fallen Byzantine Empire and its beleaged church, Bessarion, who was interested in astronomy, had a second item on his agenda and was hoping to persuade Peuerbach to take on the task of translating and commentating upon excerpts of Ptolomy’s Almagest. This was to replace a similar work which Pope Nicholas V had commissioned from the Giorgios of Trebizond and which, completed in around 1450, was found to be deficient. Due to the flourishing university and the First Viennese School of Mathematicians and Astronomers, during the fifteenth century, Vienna was the European centre for astronomy and Bessarion knew that if the job of up-dating Ptolemy’s Almagest was to be done properly he would need Peuerbach or someone of Peuerbach’s calibre. Although Bessarion was able to persuade Peuerbach to undertake the task, the astronomer died before the year was out, yet Regiomontanus had sworn to complete the task should his master fail to complete what he had started. Cancelling a series of lectures that he had been planning to give on Virgil at the university in Vienna, in the autumn of 1461, Regiomontanus and Bessarion embarked on the journey to Rome. Passing through Bologna, they then went to Ravenna, where Bessarion became so ill that he nearly died. As pointed out by David King in his Astrolabes and Angles, Epigrams and Enigmas, like Bessarion, Regiomontanus was pius and used a schematic drawing of a hill with a cross on it and two stars as an emblem on the books he owned. Both on their journey and during Bessarion’s convolesence, the two will have had plenty of time to talk and it can be assumed that Bessarion will have told Regiomontanus of a relic of the cross that he had and of an artist he knew who was painting a revolutionary series of frescos in Arezzo. Known as The Story of the Finding of the True Cross, Bessarion will have told Regiomontanus that the artist, Piero della Francesca, was also an accoplished mathematician, who like Regiomontanus, was interested in Archimedes. King further argues that a Byzantine astrolabe dating from 1062 and which is now in the Santa Giulia Museo della Città di Brescia, was brought to Italy by Bessarion. Showing it to Regiomontanus, Bessarion will have sadly observed on how, based on Ptolomy, it was out of date and inaccurate.

To cheer his sad and displaced patron up, King argues that Regiomontanus deceided to make Bessarion a new, up to date astrolabe. On the reverse side instead of engraving a hoary quadrant, Regiomontanus engraved an organum Ptolemaei which he had written about in around 1456. In Codex Yale 24, the second work by Regiomontanus is an unillustrated tract (beginning on page 255), on the quadrant as compared with an organum Ptolemaei: https://findit.library.yale.edu. As the inclusion of the organum Ptolemaei within the circle of the astrolabe left empty space, Regomontanus engraved an angel in the space above and a scroll with a dedicatory verse in the space below.

The verse translates as something approaching:

Under the protection of the divine Bessarion, called cardinal,

I arise in Rome as the work of Johannes in 1462

As the shaky Latin of the original is utterly at odds with Regiomontanus‘ consumate command of both Latin and Greek, following a series of insights made by Berthold Holzschuh, King argues that it is an acrostic, with the mistakes and out of place intervals deliberately being designed to prompt a multitude of interpretations. For the full story can be read either in book form or as a summary: www.davidaking.org.

In Rome, after presenting his Epitome of the Almagest to Bessarion, Regiomontanus wrote his work on spherical trigonometry and made a sundial for Pope Pius II.

The frontispiece of the edito precepts of Regiomontanus‘ Epitome, printed in 1496. The two men below the armillary sphere are Ptolomy (left) and Regiomontanus (right)

In 1467, he went to Hungary where he worked for Matthias Corvinus and made an astrolabe for him which has since been lost. He then settled in Nuremberg and began publihing books on astronomy. Four years after Bessarion’s death in 1472, Regiomontanus was invited by Pope Sixtus IV to Rome, to work on proposals for a reform of the calendar. Travelling to Rome, he either fell victim to a plague or as King suggests, in his Astrolabes and Angles, Epigramms and Enigmas, was poisoned and died only forty years old, in 1476.

XI. REGIOMONTANUS AND PIERO DELLA FRANCESCA?

Bessarion was close to Frederigo da Montefeltro, the Duke of Urbino and was god-father to all of the Duke’s children and when he died, it was to Fredierigo that Bessarion left his impressive library. As over the years, Piero della Francesca executed a number of works for Frederigo, Bessarion will have certainly known of him and his work. In Piero della Francesca’s The Story of the Finding of the True Cross, convincing likenesses are given of both the Byzantine Emperor Johannes VIII Palaiologos, who in the Battle between Constantine and Maximus is depicted as Constantine and of Bessarion, who in the Meeting of Solomon and Sheba, is shown as Solomon. Given the prominent nature of the theme and the acute crisis faced by the Church with respect to the falling Byzantine Empire, such references to the present are to be expected and underlie the fact that Bessarion was associated with the Bacci family who commissioned the frescos. Given the close links between Bessarion and Frederigo da Montefetro and the fact that Piero della Francesca does appear to have been in Rome and Urbino when Regiomontaus was in Italy, it is possible that, as suggested by King, they met. Alternatively, on his last journey to Rome in 1476, Regiomontaus may have seen Piero’s work on perspective which, generally reckoned to date from the 1470’ies, was held at the Ducal Library in Urbino. Either way, the unique form of quadrant given at the end of Regiomontanus‘ calendar for the years 1474, 1494 and 1513 and its occurrance in the intarsia work at the studiolo in Gubbio shows, like the letters exchanged between Jakob von Speyer and Regiomontanus, that there was a process of cultural exchange taking place between Nuremberg and Urbino and thus a reason for Regiomontanus to visit Urbino. In the Ducal Library, he will have been able to read of how, using a properly constructed system of perspective an artist can reach into the world of Platonic Forms and can correctly render the appearance of an object from any desired viewpoint.  In Piero’s treatise, Regiomontanus will have read of a „magic figure“, a form of mathematical collage that summarised the perspective projection used by an artist and which contained all the parameters necessary in order to establish a mathematically proven and true relationship between the space depicted, the pictorial plane on which the depiction was located and the viewer on the other side of the plane. On the example given below, the green square formed from the picture’s lower edge, appears on the picture plane as a red trapezoid.

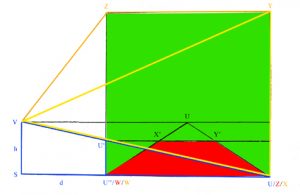
In an earlier work written by Alberti on perspective, the full extent of the relationships between the eye and what it sees and the plane of the picture, whilst implicit, has been neither worked out nor formulated. In his De prospectiva pingendi, Piero set about rectifying the matter and in doing so established what is now known as projective geometry. In the diagram given above the viewer is at distance d, away from the painting and with an eye V, that is at a height h, above the plane that reaches from the lower edge of the paining back to the horizon with a vanishing point, U. In Proposition 12 Piero says that the ratio of lengths SU:U“U is the same as VS:VU‘. This is the key to the magic figure and the system of perspective that it encapsulates and is the same as saying that the height of an object on the picture plane is inversely proportional to its distance behind the plane, with the full slate of geometrical relationships being given by the diagram below in which it can be seen that the viewer, the picture plane and what lies behind it, are all part of a single, mathematically interrelated system, with the colour-coding showing how the magic figure relates to the system as a whole.

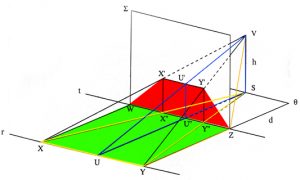Although the magic figure is an abstract summary and has only an indirect relation to the appearance of the picture and its elements, it and Proposition 12 are of immense importance as they summarise the proof given by Piero that in creating a perspective system, the painter does reach into the world of Ideal Forms described by Plato. The painter who understands perspective is thus on the same level as a philosopher or a mathematician. Nevertheless as Cusanus would have pointed out, perspective only enables artists and mathematicians to reach into the world of Ideal Forms in as far as that which is being reached out to, can be rendered in terms of straight lines. Some ten years after writing De prospectiva pingendi, Piero wrote his Libellus de cinque corpribus regularibus, or „Booklet on the Five Regular Bodies“. This was dedicated to Frederigo’s second son, Guidobaldo. In the dedication he expressed the hope that it might be placed in the Ducal Palace in Urbino in the studiolo next to the work he had written on perspective.

Like the later studiolo that the Duke had made in the Ducal Palace in Gubbio, the studiolo in the Ducal Palace in Urbino was inlaid on all sides with trompe l’oeil intarsia images. Still in situ in Urbino, among the objects depicted there are books and insruments of humanist learning as well as the Duke’s helmet and exotic things such as paraquetes in a cage, all shown in stunningly realistic perspective. It was in studiolo’s such as this that kings, dukes and princes would immerse themselves in study and learning and those inclined to philosophy would contemplate God and the Ideal Forms of Plato and his theory of the four elements, all contained within a fifth.

As establised by Euclid, the five regular Platonic Solids are the only regular solids that can be and so it was assumed that they must thus form the basis of all else that was. Here however the steps by which from the Platonic Solids, other solids were to be derived were unknown. Although the thirteen semi-regular solids known as the Archimedian Solids had been covered in detail by Archimedes, his treatise on this subject had become lost and all that was know about them was their number and appearance. In his Libellus de cinque corpri regularibus, or „Booklet on the Five Regular Bodies“, Piero showed how five of these lost solids could be constructed from out of the Platonic Solids. Had Piero and Regiomontanus met, this is likely to have been something that they would have discussed.

As partial embodyments of the Good, the Ideal Forms lead towards God, yet they are not God and cannot be God in his all-encompassing, unifing aspect. This only partial apprehension of the divine leads back to Cusanus who as seen, in his revised position concerning the gulf between that which is circular and all-encompassing and that which is straight, did find ways by which the transcendent nature of the circle could be grasped in finite, step by step ways. Like Cusanus, Piero also associated the sphere with that which was divine with the process of proceeding from the five regular solids, to the semi-regular solids and from them to solids that, with ever-increaing numbers of sides, came ever closer to the divine nature of the sphere. In his Libellus, the means by which Piero makes Archimedean Solids from Platonic Solids, is by cutting bits off the edges of the latter using a variety of techniques, one of which is division by the Golden Section. In his painting Piero was also concerned with squaring the circle and the compositions of a number of works by him have been shown to be based on squared circles. This was first established by Perry Brooks through contextual analysis and an examination of Piero’s The Resurrection and Mary Magdalen. Using geometry and with reference to Piero’s mathematical work, these insights have now been substantiated by Alexander Curtis, with the geometrical techniques used by Piero being re-discovered. Thus like Cusanus, Piero was able to reach out to the divine world of the circular and the never-ending and had he and Regiomontanus met, they may well have talked about this and how through art and astronomy, the divine could be approached. As observed in Part I, during the Antique and the Renaissance, the inclination of the Ecliptic was often thought of as being 24° or something that had been deliberately designed by God to approached this. When an equilateral triangle and a pentagon are inscribed inside a circle so that one of their corners is common to both, the difference between the common corner and the next nearest corner of the pentagon, measured in degrees from the centre of the circle, is twenty-four. From this a regular, fifteen-sided figure can be constructed with each segment spanning 24°. As the equilateral triangle was associated with the Trinity and the pentagon, which via the number five was associated with love, the inclination of the Ecliptic could be seen as a confirmation of the truth of a Neo-Platonic view of the world. That Piero was aware of this and saw it as being significant is shown by an analysis of his painting, The Baptism of Christ, by B.A.R. Carter in which it is demonstrated that these relationships are built into the composition.

In the case of a pentagon enclosed in a circle, due the fact that Phi, the number associated with the Golden Section, is related to root five, the Golden Section is written in as a natural, internal feature. For the same reasons, the same is true of an organum Ptolemei constructed within a circle, when the inclination of the Ecliptic is 24°. For Neo-Platonists of the Renaissance, this will have given confirmation that, as enigmatically hinted by Plato and Euclid, the Golden Section was the mathematical tool with which, out of continuity and change, the Demiurge had fashioned the universe. It was therefore also the key that enabled man to go beyond the confines of all that which was earthly and mortal. Taking this as a cue, an inverted Regiomontanus dial made by Alexander Curtis shows how the geometry of the above relationships are intertwined.

That such things were indeed talked about is implied by one of the cabinets depicted in the studiolo at Urbino.  Where the astronomical cabinet of the studiolo at Gubbio featured a quadrant, an armillary sphere and some books, the astronomical cabinet in the studiolo at Urbino features an armillary sphere and books shown together with an astrolabe.

The astroblabe has been identififed by David King as an astrolabe that, prior to its theft in 1977, was held by a small museum in France. An inscription on the back indicated that it was made in Urbino 1462. Signed „KP“ and with two spelling mistakes in the Latin inscriptions, the fact that it was made for use in Sicily and not Urbino, raises further questions. With respect to the inscription „KP“ a possibility suggested by King is that it stands for „Koenigsperg“ and thus for Regiomontanus who was in the region in 1461. This implies that Regiomontanus did not engrave the lettering himself and that the instrument was only completed after he had left Urbino.

In the studiolo, on the shelf below the astrolabe, there is a quill in an ink pot, a tablet and a mazzocchio, which is the roundish shape that forms the basis of a that that was popular in Florentine during the Renaissance.

Made of sew together patches of cloth, mazzocchio’s are difficult to draw in perspective. Seen as a particular challenge, in his De prospectiva pingendi, Piero della Francesca explains in detail how such a mazzocchio is to be drawn.

In the studiolo, the juxtaposition of attributes of astronomy and drawing suggests that both the drawing of things in correct perspective and the observation of the heavens with due understanding are to be seen as legitimate ways of learning about the world and thus of approaching God through an understanding of the things in his creation. Nevertheless the perseptive reader of De prospectiva pingendi perceives that, as that which is circular can never be broken down into straight lines, for all its representational power, perspective alone cannot tap into the ultimate source of the divine but rather needs an extra element, this either being the Golden Section as used by Piero in his The Resurrection and in his Libellus or the incremental procedures developed by Cusanus.